SUMAR

Consejo Editorial

Presidente
Ángel Cabezudo Bueno Coordinación editorial
Juan Guillermo Rivera Berrío

Editores
Mª José García Cebrian
Yecid E. Gaviria Restrepo
José Román Galo Sánchez
José Antonio Salgueiro

Administración web
Francisco Rodríguez Villanego y Josep Mª Navarro Canut
Código JavaScript
Joel Espinosa Longi

Colaboradores
Elena Álvarez Saiz
Carlos A. Rojas Hincapie
Edison Arbey Escobar
Ramiro A. Lopera Sánchez
Manuel Muñoz Cañadas

Diseño de portada
Julieth A. Gómez Hernández
Viñetas: klipartz.com/
Recursos interactivos:
DescartesJS
Fuentes: Lato y UbuntuMono

ISSN: 2792-4483

ARIO

Experiencias de aula

Un "domo" en el patio de recreo

José Ireno Fernández Rubio

Red Descartes 2021/Año 1, núm. 2

Tiempo necesario

Cuando se domina (no se tarda mucho, dos o tres construcciones) en una hora da tiempo a sacar el material al patio, cons- truir la cúpula, hacer una foto al grupo de alumnos constructores (como mí- nimo ocho), desmontarla y guardar el material.

Aristas

Se pueden usar de casi de cualquier material (madera, aluminio, plástico). Para que impresione y resulte atractiva recomiendo aristas a partir de 1 metro. Pueden usarse ramas de árboles aunque no vayan muy rectas, lo importante es el segmento imaginario que une los extremos.

Vértices

Recomiendo cáncamos en los extremos de las aristas y bridas reutilizables (llevan una pestaña que al presionarla se libera y puede volver a usarse ahorrándole plástico al medioambiente).

 

Un tubo de pvc usado de contenedor del material y las mochilas de los alumnos

Red Descartes 2021/Año 1, núm. 2

Proceso de construcción

El icosaedro como punto de partida.

Como se puede apreciar en la escena siguiente todos los vértices del icosaedro están en la misma superficie esférica. Si cada arista la partimos por la mitad y proyectamos ese punto medio sobre la esfera añadiendo las correspondientes aristas tenemos dos cúpulas formando una pelota. Solo resta quedarnos con la mitad.

Red Descartes 2021/Año 1, núm. 2

Pasos a dar

Empezamos uniendo 5 aristas cortas en un vértice. Nos quedarán libres los otros 5 extremos de las aristas.

En cada uno de esos extremos libres formaremos un vértice con 6 aristas (2 cortas y 4 largas). Para ello colocaremos una corta alineada con una de las cortas iniciales y dos largas a cada lado como se ve en la imagen.

Una de las largas es compartida con el siguiente vértice (consecutivo a este). Al finalizar estos 5 vértices tendremos una pirámide de base un pentágono, con 3 aristas sueltas en cada vértice de la base.

En cada uno de los extremos de las 5 aristas cortas sueltas añadiremos 4 aristas cortas. Entre medio de cada vértice de 5 aristas, formaremos vértices de 6 aristas uniendo 2 largas y 2 cortas de las que ya hay y 2 nuevas largas como muestra la imagen.

Red Descartes 2021/Año 1, núm. 2

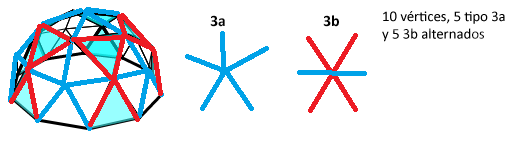
En este punto algunos alumnos deben ir sujetando la figura que se va formando levantando según necesidad y evitando que los vértices se vayan hacia adentro. Cuando esté terminado debe de quedar una figura de dos alturas que tiene como base un decágono con 2 aristas sueltas en los vértices.

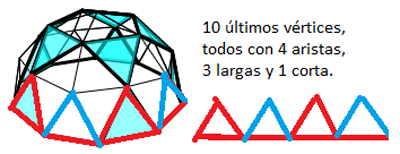
Ya solo faltan 10 vértices y añadir 10 aristas largas. En el primero de estos últimos vértices se unirán una arista larga y una corta suelta con dos nuevas largas. Para el siguiente, consecutivo al primero, sólo hará falta añadir una arista larga a tres sueltas (una de las recién puestas). Y así sucesivamente hasta llegar al último donde solo habrá que unir 4 aristas sin añadir nada.

Red Descartes 2021/Año 1, núm. 2

Problemas alrededor de la cúpula

De trigonometría

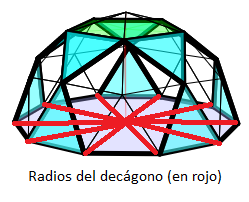
1. En un decágono regular (base de la cúpula) con lados de 1 m ¿qué longitud tiene el radio del círculo donde quedan los vértices?

Solución  Radio del decágono: 1,618 m

2. En un pentágono regular (base de la pirámide superior) con lados de 1 m ¿qué longitud tiene el radio?

Solución  Radio del pentágono: 0,85 m

Usando Pitágoras (y los resultados anteriores)

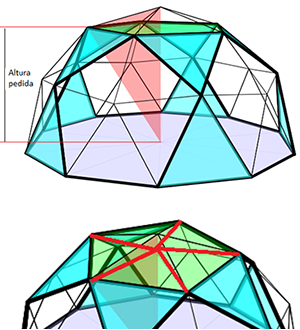
3. En la cúpula considera el triángulo isósceles de la imagen. Determina a qué altura está el vértice intermedio.

Solución  Altura: 1,376 m

4. Usando los resultados anteriores determina la longitud de las aristas laterales de la pirámide superior.

Solución  Longitud: 0,884 m

5. Calcula la altura de la pirámide superior de base pentagonal.

Solución  Altura de la pirámide:
1,618 – 1,376 = 0,242 m

Red Descartes 2021/Año 1, núm. 2

Algunas preguntas

• La cúpula se sostiene por si misma. Si construyes un icosaedro, un tetraedro o un octaedro también se sostienen. No le ocurre lo mismo al cubo. ¿por qué?
• ¿Se sostendrá el dodecaedro?
• Hayas dado o no con la respuesta, construye un triángulo y un cuadrado con este material en el suelo. A continuación sujeta una sola arista y muévela en distintas direcciones, ¿qué ocurre?

Respuestas  El triángulo es el único polígono rígido. Si añadimos un lado pierde su rígidez, y para entenderlo bien hay que construirlo.
Quiere decir que ni cuadrados, ni pentágonos, hexágonos, ... van a ser rígidos si se construyen con aristas. Este simple hecho es importantísimo en todo tipo de estructuras (puentes, gruas, torres eléctricas, vigas,…) y naturalmente en nuestra cúpula también.
La cúpula además debe su fortaleza a la esfera ya que todos los vértices están en la misma superfice esférica y eso reparte los esfuerzos (una bici no se sostiene pero sí apoyando una sobre otra).

Red Descartes 2021/Año 1, núm. 2

Red Descartes 2021/Año 1, núm. 2

Construcción en papel

Otra posibilidad es hacer la construcción en papel.

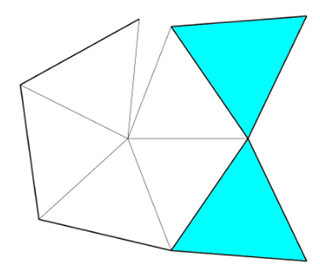
Pasos a seguir

1. Imprimir seis piezas como la de la imagen.
2. Formar las seis pirámides pentagonales blancas con dos triángulos equiláteros adosados.
3. Unir cinco de ellas formando un cercado.
4. La sexta se pega encima recortando los triángulos equiláteros azules.

Las piezas también se pueden colorear.

Red Descartes 2021/Año 1, núm. 2

A continuación se muestran dibujos diferentes y a su vez con muchas posibilidades de colorear cada uno, que se pueden imprimirPDF convertido a HTML por https://www.idrsolutions.com/..

Red Descartes 2021/Año 1, núm. 2

Programación

Pensamiento computacional:
La Micro:bit

Carlos Alberto Rojas Hincapié

Debemos tener presente que no solo con el uso de herramientas digitales podemos aprender el pensamiento computacional, es mucho más que esto, es desarrollar habilidades y formas de pensar, de explorar conceptos computacionales desde la perspectiva de su enseñanza, para ello se analizará cómo se puede usar la tecnología digital para contribuir al aprendizaje.

Red Descartes 2021/Año 1, núm. 2

Red Descartes 2021/Año 1, núm. 2

Existen diferentes códigos o lenguajes que sirven para programar, pero todos describen una secuencia lógica de pasos o instrucciones.

MakeCode es un entorno gráfico que posibilita introducirnos en el mundo de la programación de forma intuitiva a través del lenguaje visual o de bloques.

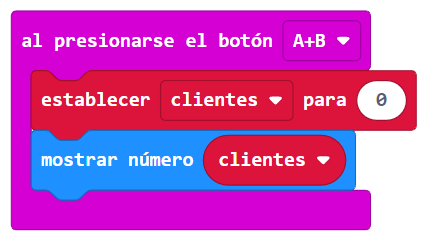
Para conocer en mayor detalle la micro:bit, identifiquemos los siguien- tes elementos que la componen:

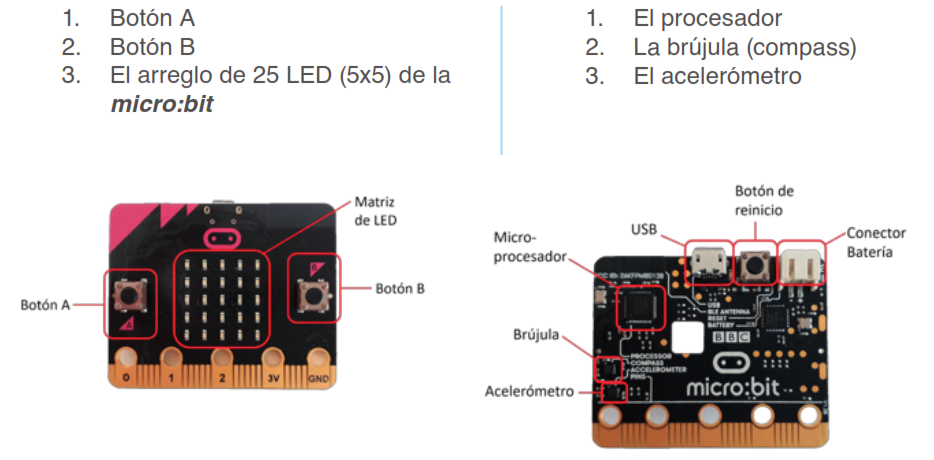
Red Descartes 2021/Año 1, núm. 2

Simulación práctica

Programemos y simulemos la siguiente situación: Carlos, de 49 años, desea seguir el impacto que tiene su actividad física en su IMC (Índice de Masa Corporal). Se quiere utilizar la micro:bit para calcular el IMC.

Este índice se calcula de la siguiente forma:

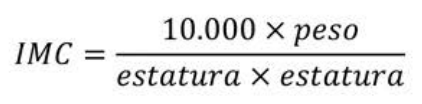
Esto es, la división del peso en kilogramos $[kg]$ sobre la estatura al cuadrado. La estatura se mide en centímetros $[cm]$. Se considera que un IMC menor de 18,5 no es bueno, corres- ponde a una persona demasiado delgada, un IMC mayor de 25 significa que la persona está en sobrepeso y un IMC de más de 30 implica obesidad.

Entre 18,5 y 25 es un IMC saludable.

El código de bloques utilizado para resolver el problema en MakeCode para programar la micro:bit que indique su IMC, para ello se propone que la micro:bit funcione así:

La estatura de Carlos es de 180 $cm$. Su peso actual es de 74 $kg$. Como Carlos ya terminó de crecer, su- ponemos que no es necesario que pueda modificar su estatura. Con estos valores podemos iniciar la simulación.

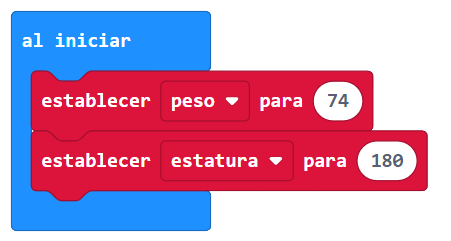
Al oprimir los botones debe mostrar:

• El botón A sube en 1 $kg$ el peso registrado.
• El botón B baja en 1 $kg$ el peso registrado.
• Al sacudir la micro:bit, el peso se reinicia en 74 $kg$.

Red Descartes 2021/Año 1, núm. 2

En el siguiente interactivo puedes observar la situación problema planteada. En la micro:bit oprimiendo los botones $A+B$ puedes observar el IMC, que al ingresarlo en el cuadro de texto derecho, mostrará el estado de salud (si no ves bien el interactivo, se sugiere ampliarlo haciendo clic en la esquina superior derecha).

(véase microbit.org, para más información).

Referencia

Programa de MINTIC-MEN-British Council. Programación para Niñas y. Niños. ACOFI-Academia Colombiana de Ciencias, Universidad Nacional de Colombia, Universidad del Norte, Colombia.https://codingforkids.cognosonline.com/

Red Descartes 2021/Año 1, núm. 2

DescartesJS

Cálculo simbólico en DescartesJSEl artículo original, publicado en https://reddescartes.org/documentacion/, tiene como título "Aplicaciones de la comunicación para integrar cálculo simbólico en Descartes".

Elena Álvarez Saiz

En este artículo se describe como interactuar con aplicaciones GeoGebra desde DescartesJS aprovechando la comunicación escena-html y la posibilidad de comunicación javascript con los applets de GeoGebra. Para ello basta realizar los tres pasos siguientes:

1. Enviar el comando considerado desde DescartesJS a una página html que contiene el applet GeoGebra.
2. Enviar este comando de la página html al applet GeoGebra y obtener por la página html su resultado.
3. Enviar el resultado desde la página html a la escena DescartesJS.

Para el paso 1 y 3 se requiere que la escena «madre» incluya un espacio HTMLIframe que permita embeber la página html contenedora del applet GeoGebra (ver artículo comunicación de una escena con el html embebido en un HTMLframe).

Para el paso 3 se utiliza el método evalCommandCAS(string) que envía el comando a ejecutar por el CAS de GeoGebra en un string y devuelve su resultado también en una cadena de caracteres.

Red Descartes 2021/Año 1, núm. 2

Para más información sobre los métodos que se pueden utilizar para interactuar con GeoGebra mediante programación javascript se puede consultar la página siguiente: comunicación de una escena con el html embebido en un HTMLframe.

El siguiente modelo muestra un ejemplo en el que se envía un comando cuyo resultado es utilizado por la escena DescartesJS. En concreto, dada una función, se obtiene su derivada e integral definida en un intervalo considerado además de obtener la circunferencia que pasa por tres puntos.

Es posible cambiar la función en el cuadro de texto y, también, el comando ejecutado, preo sólo después de haber seleccionado el cálculo a realizar; por ejemplo, escribir Integral[sen(3x)+cos(x)], luego de seleccionar Cálculo DerivadaComentario de los editores..

A continuación se presenta la documentación que explica cómo se puede modificar esta escenaPDF convertido a HTML por https://www.idrsolutions.com/..

Red Descartes 2021/Año 1, núm. 2

Con el siguiente modelo se puede ver cómo almacenar en un vector de DescartesJS el resultado de aquellos comandos que GeoGebra da como resultado una lista. En el ejemplo se obtiene los puntos de corte de dos curvas.

Red Descartes 2021/Año 1, núm. 2

A continuación se presenta la documentación que explica cómo se puede modificar la escena.

Red Descartes 2021/Año 1, núm. 2

El siguiente modelo muestra cómo obtener en una matriz DescartesJS los valores que GeoGebra devuelve como una lista de listas. En el ejemplo se calcula la matriz traspuesta de una matriz 3×3.

A continuación se presenta la documentación que explica cómo se modifica esta escena, en la que se destaca:

Red Descartes 2021/Año 1, núm. 2

Red Descartes 2021/Año 1, núm. 2

La siguiente escena muestra la sintáxis de algunos comandos para su envío desde DescartesJS a la página html que contiene el applet GeoGebra. Se incluye también un ejemplo de cada uno de ellos viendo cuál es el resultado que se obtiene.

Red Descartes 2021/Año 1, núm. 2

Ilusiones ópticas

Ilusión dinámica de Müller-Lyer

©Gianni A. Sarcone, giannisarcone.comMás información en https://www.giannisarcone.com/Muller_lyer_illusion.html

Una línea recta es el camino más corto entre dos puntos. El contexto puede jugar un papel clave en la interpretación de una línea. La ilusión de Müller-Lyer, debido al sociólogo alemán Franz Carl Müller-Lyer (1857-1916), demuestra que un segmento puede aparecer visualmente más largo o más corto si se enmarca entre dos corchetes angulares cuyos puntos se dirigen hacia afuera o hacia adentro, como lo ilustrado en la siguiente figura:

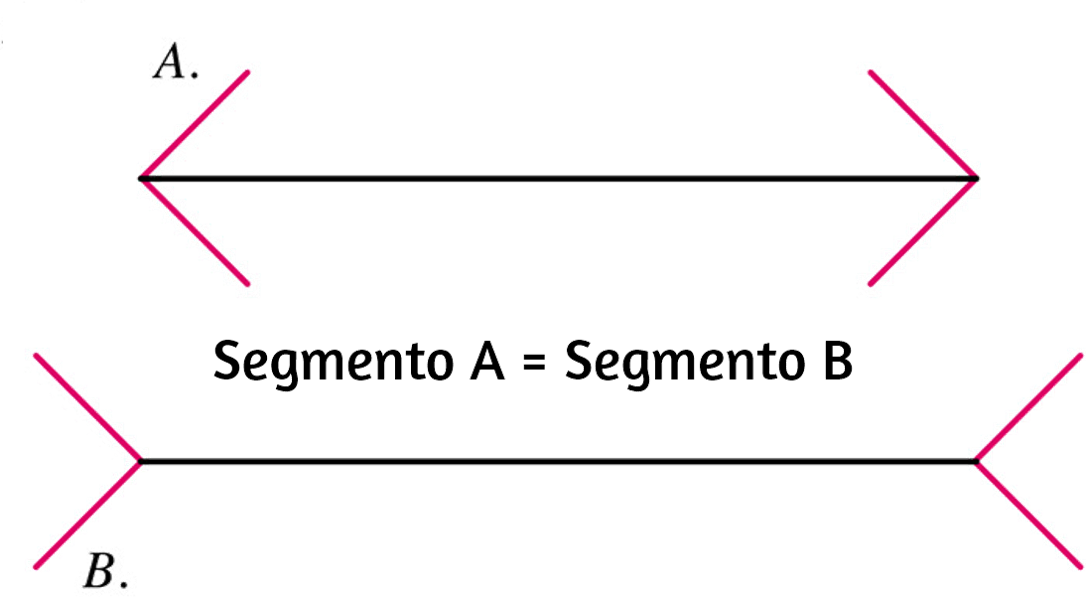
¿Qué sucede si agregamos movimiento a la ilusión? Como se muestra en el siguiente gif animado. Aunque la estrella parece pulsar, los segmentos azul y negro tienen siempre la misma longitud.

Red Descartes 2021/Año 1, núm. 2

Muchas variantes interesantes

Por extraño que parezca, la ilusión parece funcionar a pesar de que los dos segmentos que forman la línea no son rectos, como se muestra en la animación a continuación

Red Descartes 2021/Año 1, núm. 2

Red Descartes 2021/Año 1, núm. 2

Muchas ilusiones geométricas implican líneas en forma de V. Puedes ver efectos similares en los patrones de tela (ilusión de Zöllner), en la ilusión de la luna (la luna parece más grande en el horizonte debido al efecto de ilusión de Ponzo), en la distribución de una línea en un espacio cerrado (paralelogramo de Sander), etc.

Red Descartes 2021/Año 1, núm. 2

Libros interactivos

Convierte tu libro interactivo en un documento PDF

Ramiro A. Lopera Sánchez y Carlos A. Rojas Hincapie

El recurso interactivo en un libro digital

Tomando como referencia la introducción del proyecto iCartesiLibri, podemos referir que

las TIC nos han acostumbrado a las lecturas documentales hipertextuales, pero hemos de reconocer que, para los que somos inmigrantes digitales, ello nos ha representado un esfuerzo titánico o al menos muy importante, pues hemos tenido que abordar y lograr una ruptura mental anclada en la secuencialidad y reflejada en la locución “leer de pe a pa”, ello simplemente provocado porque nuestro aprendizaje fue así. Gracias a la interactividad aportada por los hiperenlaces (también se denomina URL o hipervínculo), la navegación en Internet nos permite avanzar en base a decisiones, a opciones y elecciones personales, considerarnos y ser protagonistas de nuestros avances, aunque también nos lleve a perdernos en los procelosos mares virtuales y terminemos en páginas, cuáles playas desconocidas y vírgenes, en las que una breve reflexión nos muestra que hemos encallado al encontrarnos preguntándonos: ¿pero qué es lo que yo estaba buscando?

A poco que naveguemos, de manera natural, surge la concepción y diseño de libros que contemplen la interactividad que pueden aportar las TIC, pero que eviten que ese deambular optativo finalice sin rumbo por falta de timonel. En definitiva, en una primera fase se traslada a un soporte digital el esquema antes citado y que en esta situación podemos nombrar como “elige tu propia aventura del saber”.

Red Descartes 2021/Año 1, núm. 2

Pero esa primera idea, ese diseño inicial, queda excesivamente limitado y no aprovecha el potencial educativo que aportan determinadas herramientas como la posibilidad de generar, controladamente, contenidos variables mediante la introducción de semillas aleatorias. Con esta utilidad los libros abandonan su carácter estático y evolucionan adentrándose en un dinamismo y en una variabilidad de crecimiento exponencial. Libros clásicos de matemáticas que se adentran en enseñar conceptos y procedimientos mediante ejercicios como, por ejemplo, el ampliamente usado “5000 problemas de Análisis Matemático” de Demidovich y los anti-Demidovich que surgen posteriormente, quedan conceptualmente potenciados con la pseudo-aleatoriedad, pues un ejercicio queda transformado y estructurado como un tipo de ejercicio en el que los datos y enunciados cambian cada vez que el aprendiz quiera reutilizarlo, pero lo hace de manera controlada y planificada por el autor, no se resuelve un ejercicio o se observa cómo se resuelve, sino que se aborda el análisis de situaciones tipo, adentrándonos en un aprendizaje significativo. Y ese aprendizaje puede abordarse de manera autónoma contemplando en el libro la corrección automática, es decir, integrando la posibilidad de realizar una evaluación de las respuestas del usuario, pudiéndose realizar ésta no sólo de una manera cuantitativa o correctiva, sino también formativa y así logrando reconducir posibles desviaciones provocadas por una incorrecta elección o valoración en la respuesta aportada por el lector/actor.

Los nuevos libros también permiten incluir contenido multimedia que facilita la exposición y la conformación de conceptos, pues estos media permite mostrar tanto el mundo, la realidad que es objeto de estudio, como su modelo conceptual o simplificado que facilita el análisis y obtención de conclusiones, es decir, nos ubica en el modelo académico teórico, pero siempre contextualizado (iCartesiLibri).

Las escenas de Descartes son recursos interactivos que pueden insertarse o embeberse en múltiples soportes y medios como páginas web, blogs, wikispaces o plataformas de aprendizaje como Moodle, entre otras herramientas.

Red Descartes 2021/Año 1, núm. 2

Estas posibilidades de integración permiten el uso de los recursos elaborados con Descartes en cualquier entorno educativo bien presencial o bien a distancia, integrándose de manera natural en cualquier planteamiento metodológico y contexto tecnológico. Estas escenas permiten el desarrollo de modelos en los que el usuario puede interactuar y la respuesta automática que se presenta como consecuencia de esa interacción genera relaciones cognitivas que permiten un aprendizaje significativo. Son muy diversos los objetos que pueden integrarse e interrelacionarse en las escenas de Descartes contemplándose tanto representaciones bidimensionales como tridimensionales.

Un ejemplo de interactividad es este recurso que nos presenta la ilusión de Marilyn-Einsten, muy viral años atrás, diseñado por Sharjeel Yunus, usa una imagen fija que se puede volver borrosa (barra de difuminación), de tal forma que se pierdan los detalles y se logre el mismo efecto de verla pequeña o lejana Veáse el libro Percepcíon Visual (página 218)..

Red Descartes 2021/Año 1, núm. 2

Otra ilusión bastante conocida, es la de movimiento "Stepping feet", en esta los bloques avanzan de forma horizontal entre líneas verticales. Parece que se van parando, como si dieran pasos, pero no. Ni se detienen ni cambian de

velocidad en ningún momento. El profesor de la Universidad de California San Diego Stuart Anstis es el autor de esta ilusión óptica. En su página web explica que cuando el bloque azul se encuentra en las franjas negras, su contraste es bajo, por lo que el movimiento se ve más lento. En las franjas blancas, los bordes tienen un contraste alto, por lo que el movimiento parece acelerarse. Con el bloque amarillo se da el mismo efecto, pero al revés (https://verne.elpais.com).

Pero, ¿si deseamos generar un documento PDFEn 1991, el cofundador de Adobe, el Dr. John Warnock, inició la revolución que marcaba el paso del papel al formato digital con una idea que bautizó como “The Camelot Project” (el proyecto Camelot). El objetivo consistía en que todo el mundo pudiera capturar documentos de cualquier aplicación y enviar la versión electrónica de dichos documentos a donde quisiera, así como verlos e imprimirlos desde cualquier máquina. En 1992, el proyecto Camelot ya había pasado a convertirse en PDF. Hoy en día, es el formato de archivo en el que las empresas de todo el mundo depositan su confianza. que conserve estas interacciones? Primero vamos a entender qué es el formato PDF y su contexto.

¿Qué es el formato PDF?

De acuerdo a la plataforma Adobe.com, los archivos PDF dirigen el mundo. Sus letras corresponden a las siglas traducidas del inglés formato de documento portátil (más conocido por la sigla PDF), para presentar e intercambiar documentos de manera fiable, independientemente del software, el hardware o el sistema operativo.

Red Descartes 2021/Año 1, núm. 2

El PDF es ahora un estándar abierto, reconocido por la Organización Internacional para la Estandarización (ISO). Los documentos PDF pueden contener vínculos y botones, campos de formulario, audio, vídeo y lógica empresarial. Se pueden firmar electrónicamente y puedes ver con facilidad los archivos PDF en Windows o Mac OS utilizando el software gratuito Acrobat Reader DC.

Convertir el libro interactivo en un documento PDF interactivo

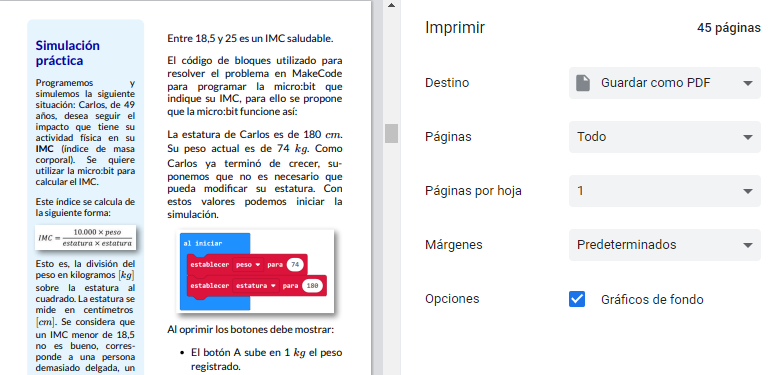
Ahora veremos cómo se realiza la conversión del libro interactivo en formato HTML a un archivo en pdf interactivo. Inicialmente, hay que generar un primer documento PDF desde navegadores como Opera, Edge o Chrome (en Firefox no se genera bien). Veamos, como hacerlo desde Chrome.

Desde la barra de menú o con clic derecho seleccionamos la opción de imprimir.

Red Descartes 2021/Año 1, núm. 2

El destino es un PDF (guardar como PDF), pero debes tener activada la casilla de gráficos en segundo plano, para garantizar que los gráficos e imágenes se muestren en el PDF.

Una vez generado el documento PDF se observa que las escenas interactivas y videos no se muestran, solo vemos un recuadro como el de la figura derecha.

Para incorporar las imágenes de los interactivos y videos, seguimos los siguientes pasos:

1. Guardamos el archivo index.html con otro nombre, por ejemplo pdf.html, en el cual modificaremos los códigos, y así no dañar accidentalmente el archivo original.
2. Capturamos las imágenes donde se encuentran las escenas interactivas y los videos; para ello, podemos utilizar la herramienta que nos proporciona Windows como es Recortes (WIN + SHIFT + S), aunque podemos encontrar diferentes herramientas para esto. Procedemos a guardar las imágenes, creando una carpeta llamada pdf (nombre opcional) dentro del directorio de nuestro libro interactivo. Se sugiere que el nombre de la imagen sea el número de la página donde se encuentra el libro, por ejemplo p8.png.

Red Descartes 2021/Año 1, núm. 2

3. Abrimos el archivo pdf.html con un editor HTML (Notepad++, Sublime text, etc.) y buscamos las páginas donde se encuentran los códigos de las escenas interactivas o videos y lo convertimos a una imagen con el hiperenlace donde se encuentra publicado, para esto se utiliza una etiqueta párrafo de la siguiente forma :
   <p style="text-align:center"> <a target="_black" href="Enlace del interactivo"> <img src="Ubicación de la imagen almacenada" width="100%"/></a></p> Para ello, se debe tener presente que el libro debe estar publicado previamente en un servidor, por ejemplo, en el Proyecto iCartesiLibri, eshostVéase el siguiente video, para mayor información de eshost., entre otros.

Realizamos el mismo proceso para todas las escenas interactivas y videos que se tengan en el libro y guardamos el libro que nombramos pdf.html con todos los cambios.

Por último, abrimos el archivo html del libro modificado en el navegador y procedemos a generar el PDF con la opción de imprimir con el procedimiento mencionado anteriormente, lo guardamos como libro_interactivo.pdf o como se desee nombrar.

Para verificar los cambios abrimos el PDF en cualquier navegador, en el lector Acrobat o en otros lectores como Foxit Reader que es de código abierto, observa que donde se tenían las escenas interactivas se verán las imágenes guardadas de cada interactivo conservando los tamaños y al sobreponer el puntero del ratón, este cambia indicando que hay un hiperenlace, el cual al hacer clic cargará la escena en una ventana emergente o página nueva.

Red Descartes 2021/Año 1, núm. 2

Algunas recomendaciones de uso del navegador:

• Chrome: Al hacer clic sobre la imagen que carga el interactivo nos muestra la escena sacándonos del libro o página donde estabamos, para evitar esto oprimimos Shift+clic, mostrando la escena en una ventana emergente y evitamos perder el hilo del libro. Con CTRL+clic la escena se abrirá en otra pestaña.
• Firefox: Similar a Chrome, excepto que al hacer clic sobre la imagen que carga el interactivo lo abre en la misma ventana y si se pulsa atrás vuelve al PDF sin perder el hilo del libro.
• Opera: Funciona como el navegador de Chrome, pero las ventanas emergentes son centradas en la pantalla.

Por último, si deseas más información, observa el siguiente video:

Red Descartes 2021/Año 1, núm. 2

DescartesJS

Elemento gráfico "cara" en espacios 3D de DescartesJS y el sistema diédrico

Juan Guillermo Rivera Berrío

En este artículo mostramos cómo se pueden diseñar perspectivas isométricas y las proyecciones ortogonales (vistas) principales frontal, superior y lateral (alzado, planta y perfil) de una pieza, usando el espacio 3D del editor DescartesJS y el elemento gráfico "cara".

Antecedentes

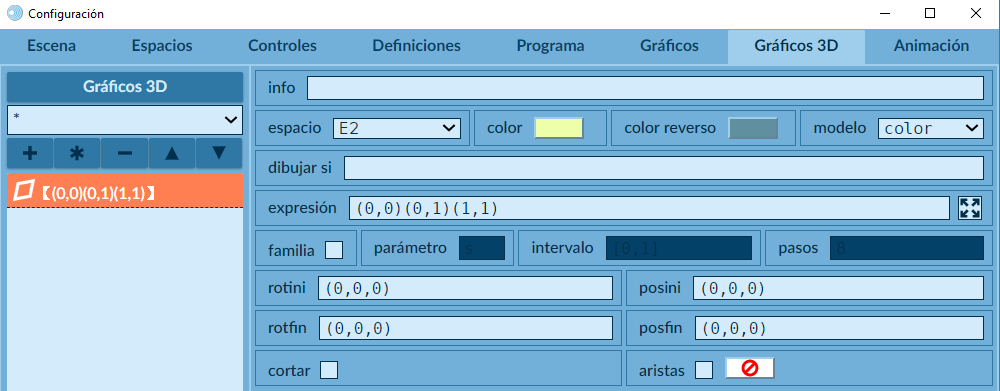
El editor DescartesJS, mediante su selector “Gráficos 3D”, permite la inserción de caras poliédricas a partir de polígonos que se definen indicando sus vértices como pares ordenados $(x_1, y_1), (x_2, y_2)$, $\cdots, (x_n, y_n)$, tal como se indica en la siguiente imagen:

Red Descartes 2021/Año 1, núm. 2

El desarrollador de la escena interactiva lo ubica en el sitio deseado mediante un cambio de posición y rotación usando los parámetros rotini, posini, rotfin y posfin. Este procedimiento se vuelve complejo para abordar el diseño de las caras (vistas) de una pieza en un sistema diédrico. Accidentalmente, hemos descubierto que el editor acepta, también vértices con tres coordenadas $(x_1, y_1, z_1), (x_2, y_2, z_2)$, $\cdots, (x_n, y_n, z_n)$, es decir, ubicándolos directamente en el espacio, aunque hay que ser precavidos para que efectivamente sean puntos coplanarios y determinen estrictamente una cara (veáse Documentación de Descartes JS) Esto conlleva la ventaja de no tener que manipular los parámetros rotini, posini, rotfin y posfin para orientar la cara, que puede resultar más complicado (Ibid, pág 57).. Gracias a este descubrimiento, es posible diseñar la siguiente pieza con sólo nueve polígonos:

Red Descartes 2021/Año 1, núm. 2

Las caras de la pieza anterior, se diseñaron así:

• Caras de color blanco:
  $(0,0,0)(0,0,4)(0,2,4)(0,2,2)(0,4,2)(0,4,0)(0,0,0)$, $(0,0,0)(0,0,4)(2,0,4)(2,0,2)(4,0,2)(4,0,0)(0,0,0)$
  y $(0,0,0)(0,4,0)(4,4,0)(4,0,0)(0,0,0)$,
  la última (vista inferior) es un cuadrado.
• Caras de color rojo:
  $(2,0,4)(2,2,4)(2,2,2)(2,0,2)(2,0,4)$
  y $(4,0,2)(4,4,2)(4,4,0)(4,0,0)(4,0,2)$
• Caras de color verde:
  $(0,2,4)(0,2,2)(2,2,2)(2,2,4)(0,2,4)$
  y $(0,4,2)(0,4,0)(4,4,0)(4,4,2)(0,4,2)$
• Caras de color turquesa:
  $(0,0,4)(0,2,4)(2,2,4)(2,0,4)(0,0,4)$
  y $(2,0,2)(2,2,2)(0,2,2)(0,4,2)(4,4,2)(4,0,2)(2,0,2)$

Sistema diédrico

El sistema diédrico es un método de representación geométrica de los elementos del espacio tridimensional sobre un plano, es decir, la reducción de las tres dimensiones del espacio a las dos dimensiones del plano, utilizando una proyección ortogonal sobre dos planos que se cortan perpendicularmente. El sistema formado por los dos planos se denomina diedro. Para generar las vistas diédricas, uno de los planos se abate sobre el segundo, permitiendo la representación de las proyecciones de los elementos en un plano (https://es.wikipedia.org/wiki/).

A continuación presentamos algunos ejemplos que muestran la vistas principales de un objeto (proyecciones ortogonales).

Red Descartes 2021/Año 1, núm. 2

Son 37 piezas tomadas de diferentes ejercicios propuestos en los primeros cursos de Dibujo Técnico o de Perspectiva IsométricaAlgunos ejercicios fueron tomados de http://www.educacionplastica.net/, y otros de https://sketchfab.com/pelandintecno/.. Antes de presentarlos, es importante comprender que una proyección ortogonal es la que se observa al mirar en forma directa un lado o "cara" de un objeto, tal como se muestra en la siguiente escena interactiva:

Rota la pieza para observar que las proyecciones ortogonales coinciden con lo que observas en cada una de las caras de la pieza.

Para los ejemplos, sólo se muestran las caras frontal (alzado), lateral izquierda (perfil) y cara superior (planta). Ellas son suficientes para poder reconstruir cualquier pieza.

Red Descartes 2021/Año 1, núm. 2

Piezas 3x3x3

Son seis piezas que tienen dimensiones de $3\cdot3\; u^2$ en planta y $ 3\; u$ de altura. En la siguiente tabla haz clic en cualquiera de las imágenes, para acceder al interactivo.

Pieza 20	Pieza 21	Pieza 22
Pieza 24	Pieza 25	Pieza 26

En cada pieza trata de observar las vistas principales, luego haz clic en los botones correspondientes, para verificar tu hallazgo.

Piezas 4x4x4

Son 17 piezas que tienen dimensiones de $4\cdot4\; u^2$ en planta y $ 4\; u$ de altura. En la siguiente tabla hemos puesto sólo nueve piezas pero, al final, podrás interactuar con todas las piezas. Haz clic en cualquiera de las imágenes, para acceder al interactivo. El interactivo, si lo deseas, lo puedes ver en pantalla completa.

Red Descartes 2021/Año 1, núm. 2

Pieza 17	Pieza 18	Pieza 19

Pieza 31	Pieza 32	Pieza 33

Pieza 37	Pieza 38	Pieza 39

Piezas 4x5x4

Son 12 piezas que tienen dimensiones de $4\cdot5\; u^2$ en planta y $ 4\; u$ de altura. En la siguiente tabla puedes interactuar con seis piezas. Como práctica, trata de dibujar las vistas principales en un papel; para ello, activa la cuadrícula para una mejor identificación de las proyecciones ortogonales.

Red Descartes 2021/Año 1, núm. 2

Pieza 42	Pieza 44	Pieza 45
Pieza 46	Pieza 47	Pieza 48

Con el elemento gráfica "cara", pudimos diseñar, relativamente fácil, las piezas anteriormente descritas. Usando otros elementos como el cilindro, se pueden obtener piezas como:

Red Descartes 2021/Año 1, núm. 2

Finalmente, en la siguiente escena interactiva, diseñada en DescartesJS, puedes interactuar con 37 piezas. Ten un poco de paciencia con la carga de imágenes.

Red Descartes 2021/Año 1, núm. 2

Ilusiones acústicas

Ilusiones acústicas o auditivasEste artículo ha sido tomado del libro Percepción Visual (página 212). Al leer y comprender la ilusión acústica, podrás conlcuir que la percepción visual influye, también, en la percepción acústica.

Juan Guillermo Rivera Berrío

La Real Academia Española (RAE) define "ilusión" como un concepto, imagen o representación sin verdadera realidad, sugeridos por la imaginación o causados por engaño de los sentidos. Así las cosas, podemos tener ilusiones ópticas, auditivas, táctiles, olfativas y gustativas, pues podemos experimentar, con nuestros cinco sentidos, sensaciones que no son reales.

Con respecto a las ilusiones auditivas, Diana Deutsch nos explica que "el cerebro está constantemente tratando de encontrar significado a las cosas, incluso cuando no hay significado; por ello, cuando se nos presentan sonidos ambiguos, podemos escuchar palabras y frases que realmente no están allí" (http://philomel.com/phantom_words/).

Palabras fantasma

Es precisamente Diana Deutsch (Universidad de California, San Diego) quien demuestra esta ilusión. A continuación, podrás escuchar estas ilusiones estéreo a través de altavoces, es importante colocar los altavoces uno a la izquierda y el otro a la derecha. Según Deutsch, el efecto funciona particularmente bien en un aula o auditorio; sin embargo, lo hemos probado con sistemas de audio estereo corrientes, pudiendo apreciar o, si se quiere, percibir la ilusión.

Red Descartes 2021/Año 1, núm. 2

Hemos dispuesto los audios en escenas diseñadas con DecartesJS, de tal forma que puedas realizar una de dos actividades. La primera, consiste en escuchar el audio y pensar en la palabra que aparece en pantalla, es casi seguro que alguna de ellas se convertirá en una palabra fantasma que escucharás repetidamente. La segunda actividad, es cerrar los ojos y tratar de escuchar la palabra que nuestro cerebro trata de construir, pese a que esta no exista en la grabación.

He aquí el primer audio de Diana Deutsch:

Como lo decía el filósofo William James (para algunos, el padre de la psicología): "la percepción es un proceso", en la que se discute sobre las cualidades reales y aparentes de un objeto, éstas últimas ejemplarizadas con el sonido de un coche de caballos; por ello, cada persona tiene tiempos de percepción diferentes y, en el audio de la escena, es posible que para algunos el tiempo dado en cada palabra no haya sido suficiente, por lo que reiniciar la escena, cerrar los ojos y pensar en una palabra (bueno, por ejemplo), sea una buena idea.

Red Descartes 2021/Año 1, núm. 2

Habrás notado que hemos puesto una frase en inglés. Según la investigadora Deutsch, los audios se prestan a que cualquier persona, sin importar su idioma, identifique alguna palabra.

Si el inglés es su segundo idioma, es posible que algunas de las palabras que escuche estén en su idioma nativo. Por ejemplo, los hablantes nativos de chino a veces escuchan palabras en chino, y los hablantes nativos de español a veces escuchan palabras en español. Esta impresión puede ser tan fuerte que la gente a veces se convence de que se han insertado palabras tan "extranjeras" en las pistas, aunque en realidad esto nunca sucede. Además, las palabras que se escuchan a menudo parecen ser pronunciadas por diferentes voces, cada una de las cuales tiene una cualidad distintiva. Ocasionalmente, las personas escuchan tonos musicales u otros tipos de sonido mezclados con las palabras (http://philomel.com/phantom_words/).

Puedes escuchar otras tres grabaciones, haciendo clic en las siguientes imágenes. Cada una de ellas se han ajustado al mismo modelo anterior.

No olvides usar dos altavoces, pues en los audios cada pista contiene dos palabras o una sola palabra que se compone de dos sílabas, y estas se repiten una y otra vez.

Red Descartes 2021/Año 1, núm. 2

La secuencia idéntica se reproduce a través de ambos altavoces simultáneamente, pero cuando el primer sonido proviene del altavoz de la izquierda, el segundo sonido proviene del altavoz de la derecha; y viceversa (Ibid).

Oímos lo que esperamos oír

En el primer trimestre de 2021 se hizo viral, en Twitter y en TikTok, la ilusión acústica generada por un audio grabado por una mujer que, para algunos, se oye como “Hija, ¿llevaste la plata del alquiler al padrino?” o, para otros, “Hija, llevaste la plata de la bicicleta al padrino?”.

En el interactivo anterior, lee la palabra que aparece en la escena, concéntrate en ella y, seguramente, la escucharás. Lo de "seguramente" es una afirmación válida, pues los estudios científicos al respecto, como explicamos a continuación, así lo afirman.

Red Descartes 2021/Año 1, núm. 2

Luego de muchas posibles explicaciones, que inician con los aspectos técnicos como el nivel de agudos o graves con el que se escucha el audio, pasando por una supuesta manipulación de la grabación y terminando con explicaciones más complejas desde la neurociencia, se supo que fue Karina Nicolini quien envió un audio a su hija Camila con la frase "Hija, llevaste la plata de la bicicleta al padrino?”; es decir, la palabra correcta es "bicicleta".

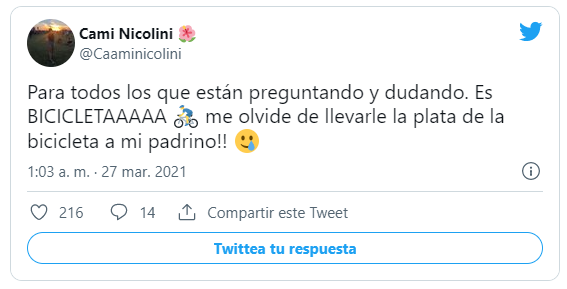
La explicación la encontramos en el efecto McGurkEl efecto McGurk (Harry McGurk), también es conocido por su artículo "escuchar los labios y ver las voces"., que es otro factor que incide en el fenómeno de la percepción, el cual se genera por una deficiencia del audio percibido, bien sea por la presencia de ruidos o por una pronunciación deficiente o muy rápida, como el caso de Karina. Ante esta situación, el cerebro busca ayuda para entender o percibir el estímulo que llega, recurriendo a perceptos previos almacenados en la memoria, de no obtener esa ayuda, simplemente se puede oir cualquier cosa; sin embargo, como ocurrió con Karina, aparecen posibles palabras que ayudan a percibir el audio, palabras que se constituyen en una imagen mental.

Red Descartes 2021/Año 1, núm. 2

Esta interacción entre la audición y la visión hacen que el cerebro le preste más atención al estímulo más nitido, que para nuestro ejemplo es la imagen de la palabra "bicicleta" o "alquiler", bien sea porque se vea escrita como en el interactivo o porque "se vea mentalmente". Es así como se produce la ilusión, "cuando el componente auditivo de un sonido está emparejado con el componente visual de otro sonido, dando lugar a la percepción de un tercer sonido" (https://www.lavanguardia.com/).

El efecto McGurk debe definirse como un cambio categórico en la percepción auditiva inducida por el habla incongruente, lo que resulta en una única percepción de escuchar algo diferente a lo que dice la voz. En segundo lugar, al interpretar el efecto McGurk, es fundamental tener en cuenta la percepción de los componentes del estímulo visual y el acústico unisensorial (Tiippana, 2014).

El efecto McGurk es más notable cuando escuchamos a alguien y, a la vez, vemos sus labios. En algunos experimentos, una persona pronuncia, con los labios, la sílaba "Ba" varias veces y escuchamos "Ba", pero si lo hace juntando el labio inferior con los dientes superiores, escuchamos "Fa", pese a haber pronunciado "Ba".

Imagen del vídeo https://www.youtube.com/watch?v=lEoY2e-pB5w

Pero, si no escuchas "Fa", según los estudios experimentales, es porque tienes un daño cerebral o algún desorden mental... por ello, lo de la afirmación "seguramente".

Red Descartes 2021/Año 1, núm. 2

Visual art

Kinegrams, Art in Motion!

©Gianni A. Sarcone, giannisarcone.comGianni A. Sarcone es un artista visual y autor de columnas y artículos para periódicos y revistas. Ha escrito libros en varios idiomas sobre entrenamiento cerebral, pensamiento crítico, arte visual y sobre el mecanismo de la visión. Fundó Archimedes 'Lab Project™ (https://archimedes-lab.org/). En 2018, ganó el prestigioso Premio del Libro Joven de la Royal Society.

During the 1960’s, the Op Art (short for Optic Art) movement began experimenting with pictures that stimulate the brain in such a way that they appear to move. It is around 1997 that I started developing optic kinetic media called 'Kinegrams'. With my kinetic technique based on early optical principles it is possible to transform everyday objects into little movie machines… These optical applications produce true amazing effects with simple phase-motion patterns and overlays having thin black pattern printed on them - rivaling the classic motion picture toys of a century ago!For more information see https://www.giannisarcone.com/Kinegrams.html.

How it works

All animation is based on the same principle: persistence of vision. The Kinegrams artfully combine the visual effects of moiré patterns with the zoetrope animation technique. The earliest attempts of this technique date back to the French pre-cinema technique of “Ombro-Cinéma” in the late XIX Century. The animated sequence is created when the complex image - the Kinegram - is viewed through the acetate overlay with a solid black pattern printed on it.

Red Descartes 2021/Año 1, núm. 2

The blank spaces of the pattern being transparent, as the overlay is slid across the Kinegram, different sections of the Kinegram become visible... Your brain links this succession of appearing images together, creating the illusion of fluid motion.

Sampling and applications

Kinegrams can be used in books, animated cards, works of art, interior design, and on many other products. Below are some Kinegram samples you can play or experiment with.

Playing with words

Kinegrams are highly interactive and can be a smart way to teach and promote the pleasure of reading to children. In effect, they allow words to become alive and to poetically transform into images, and viceversa, catching the curiosity and attention of youngsters and adults alike.

Red Descartes 2021/Año 1, núm. 2

In the following interactive scene observe the effect of rotational movement with the word Rotor (Click in the upper right corner to interact in a larger window):

Playing with shapes

Kinegrams represent a dynamical and amazing way to investigate the many aspects of shapes and colors. With this technique, hypnotic abstract shapes and patterns appear to move in a loop-like seamless fashion.

In the following interactive scene, see colored ropes that seem to wind and unwind.

Red Descartes 2021/Año 1, núm. 2

Capturing the emotions and instant of everyday life

Any everyday life act or gesture can be visually simulated by Kinegrams: walking, dacing, swimming, flying... Like a very short yet significant film!

Finally, in the following interactive scenes, see a pretty girl who apparently loves to dance and, in addition, a mysterious woman who paints her lips.

Red Descartes 2021/Año 1, núm. 2

Red Descartes 2021/Año 1, núm. 2

The editors of the magazine present other kinegrams designed by Keith Enevoldsen under Creative Commons Attribution-ShareAlike 4.0 International License:

Red Descartes 2021/Año 1, núm. 2

Libros interactivos

Red Descartes 2021/Año 1, núm. 2

Red Descartes 2021/Año 1, núm. 2

Portada, datos legales y tabla de contenido del libro interactivo "Curvas Polares".

Red Descartes 2021/Año 1, núm. 2

Red Descartes 2021/Año 1, núm. 2

Red Descartes 2021/Año 1, núm. 2

La evaluación dada por los estudiantes se aprecia en la siguiente figura:

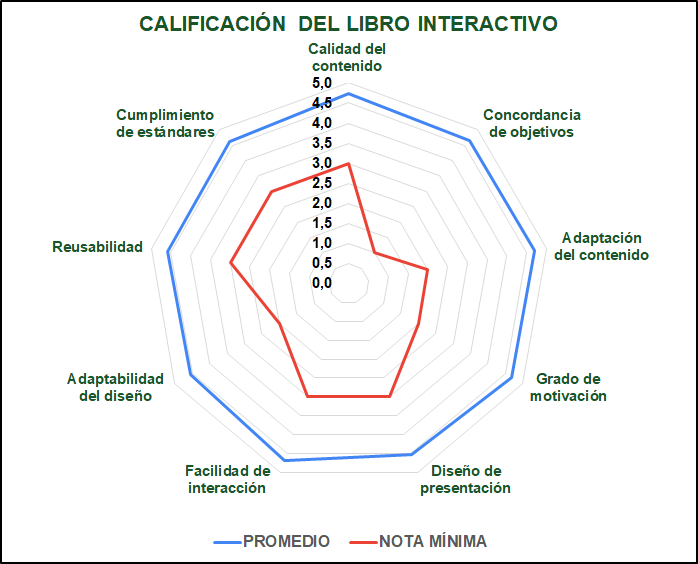
Resumen gráfico de la evaluación del libro "Curvas Polares".

Red Descartes 2021/Año 1, núm. 2

Red Descartes 2021/Año 1, núm. 2

Red Descartes 2021/Año 1, núm. 2

Red Descartes 2021/Año 1, núm. 2

Difusión

Planifica el nuevo curso con los recursos interactivos de Proyecto Descartes Los primeros apartados de este artículo están referidos al sistema educativo español, aunque es fácilmente adaptable al del resto de países.

José Antonio Salgueiro González

Una vez más, desde la RED Descartes comenzamos el curso escolar 2021/2022 con ilusión, entusiasmo y emoción, atributos que esperamos transmitir a todos los agentes que intervienen en la educación. Por todo ello, ofrecemos el acceso gratuito a nuestros recursos para el personal docente, el alumnado y sus familias, unos recursos interactivos que han demostrado su gran utilidad tanto en la enseñanza presencial como en la enseñanza a distancia.

Esperamos que desde cualquier lugar del mundo, y a cualquier hora,

Red Descartes 2021/Año 1, núm. 2

solos o acompañados, los recursos ofrecidos sean de la mayor utilidad posible para aprender a aprender, para fomentar la iniciativa emprendedora, para desarrollar la autonomía personal y todas las competencias y habilidades que corresponden en la Escuela del s. XXI.

Educación infantil (hasta los 6 años)

Para la etapa de infantil ofrecemos, en primer lugar, una pequeña colección de recursos interactivos del Proyecto Canals, basados en los materiales manipulables de María Antonia Canals, que es un referente y su experiencia y práctica educativa una guía para el desarrollo de buenas acciones formativas.

Como ejemplo, hemos seleccionado el recurso "Juegos con cantidades", cuyo objetivo es trabajar de una manera muy directa la noción de cantidad, por comparación de grupos de objetos y correspondencia entre sus elementos.

Red Descartes 2021/Año 1, núm. 2

Las comparaciones se basan no en las grafías de los números, que no aparecen, sino en motivaciones de lógica. Así facilitan que los niños y niñas entren en el mundo de los números por su verdadero significado, y no por el único camino del reconocimiento de números escritos.

También ofrecemos una importante colección de recursos del proyecto "Aplicación de Juegos Didácticos en el Aula", que han sido diseñados por maestros y maestras de infantil en diversos cursos de formación, todos validados en el aula.

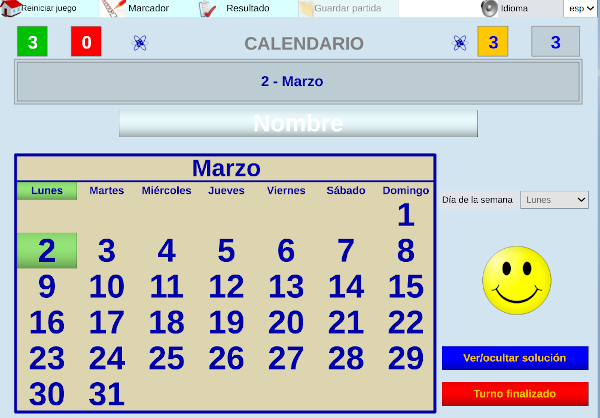
Como ejemplo, hemos seleccionado el recurso "Calendario", que permite, desde la pizarra interactiva en equipo o de forma individual en un dispositivo móvil, identificar el día de la semana en un calendario.

Recomendamos conocer el proyecto de innovación educativa "Comprensión matemática con material manipulativo", aprobado por

Red Descartes 2021/Año 1, núm. 2

la Consejería de Educación y Deporte de la Junta de Andalucía para la formación del profesorado en matemáticas.

Finalmente, en la imagen inferior, encontramos el acceso al catálogo completo y actualizado de recursos interactivos para infantil, accesibles desde cualquier dispositivo móvil, ordenador personal, portátil o pizarra digital.

Red Descartes 2021/Año 1, núm. 2

Educación primaria (de 6 a 12 años)

Mucho más amplia y diversa es la oferta de recursos interactivos para esta etapa educativa, con la implicación de varios subproyectos de RED Descartes y que depende del curso al que van dirigidos. Así, ofrecemos 360 objetos de aprendizaje interactivos para Matemáticas de 1º a 6º del Proyecto Canals (Canales cartesianos hacia el conocimiento), a los que podemos acceder desde la imagen siguiente:

También podemos encontrar contenedores con variadas actividades de autoevaluación para Matemáticas y Lengua con el Proyecto Plantillas, un proyecto con el que cualquier docente puede generar recursos interactivos de Descartes sin necesidad de ser experto cartesiano.

Red Descartes 2021/Año 1, núm. 2

Por otra parte, disponemos de recursos para Matemáticas en el Proyecto Unidades Didácticas (bloques de programación docente, base del desarrollo del proceso de enseñanza y aprendizaje y que integran una metodología y una planificación temporal para la consecución de los objetivos contemplados) o en el Proyecto Miscelánea (escenas aisladas que tratan aspectos muy variados del currículo de Matemáticas y que pueden servir para que el profesorado las utilice directamente para ilustrar conceptos y técnicas básicas, o para que construyan con ellas actividades y propuestas de trabajo en el aula).

Llegamos a los libros interactivos, que permiten al alumnado aprender y practicar de forma autónoma la operatoria básica:

Red Descartes 2021/Año 1, núm. 2

La suma	La resta	Fracciones

Específicamente, para el tercer curso, ofrecemos una colección de objetos para el aprendizaje competencial basados en las pruebas de Evaluación de Diagnóstico LOMCE. En esta sección se enlazan los recursos en dos modalidades: una versión dinámica que sigue la pauta intrínseca del Proyecto Descartes y una versión original estática que formula los estímulos y preguntas de acuerdo a lo expresado en el documento original que sirvió de guía en este desarrollo.

Podemos acceder a los recursos del Proyecto Competencias para 3º desde la siguiente imagen:

Red Descartes 2021/Año 1, núm. 2

De forma completamente análoga, existe otra colección de objetos para el aprendizaje en competencias en el cuarto curso, unos materiales basados en las pruebas de Evaluación de Diagnóstico LOE.

Podemos acceder a los recursos del Proyecto Competencias para 4º desde la siguiente imagen:

El proyecto "Pizarra Interactiva" surge con el propósito de desarrollar recursos educativos digitales interactivos para el tercer ciclo, 5º y 6º de la Educación Primaria, en las áreas curriculares de Lengua Castellana y Matemáticas, que están diseñados para un uso preferente en la pizarra digital, pero siendo también susceptibles de usar en cualquier ordenador personal. Todos los objetos cuentan con un diseño común y están estructurados como secuencias didácticas que cubren un proceso completo de enseñanza/aprendizaje con cuatro pasos: Introducción, Exploración, Ejercicios y Evaluación. Las pautas seguidas en el diseño de los objetos de aprendizaje contemplan la realimentación inmediata, el aprendizaje significativo, el predominio de la interactividad, la disponibilidad de un contador de aciertos y fallos y el uso de semillas aleatorias las cuales permiten

Red Descartes 2021/Año 1, núm. 2

reutilizar el mismo objeto, pero cada vez con diferentes datos obligando a que el alumnado necesite prestar atención, tenga que leer y esté forzado a reflexionar sobre lo leído, por tanto contribuye a que aprenda practicando y que pueda practicar tanto como quiera con diferentes situaciones y cuestiones.

El índice temático para Matemáticas comprende los bloques dedicados a Números y operaciones, Medidas, Geometría y Estadística.

Por su parte, para el área de Lengua se tratan los bloques de contenidos relativos a Gramática, Vocabulario, Ortografía y Escritura.

Podemos acceder a todos los recursos del Proyecto Pizarra Interactiva desde la siguiente imagen:

Red Descartes 2021/Año 1, núm. 2

El Proyecto @prende.mx es una iniciativa de la Secretaría de Educación Pública del gobierno mejicano a través de la cual busca la introducción de las TIC en la Educación. El Gobierno Federal de México proporciona materiales y recursos didácticos que apoyan al alumnado en sus procesos de estudio en el hogar y en la escuela

El proyecto ofrece recursos interactivos para Matemáticas, Ciencias y Castellano.

Podemos acceder a todos los recursos del Proyecto @prende.mx desde la siguiente imagen:

Llega el momento para el área de Ciencias Sociales con el Proyecto GEOgráfica, que tiene como objetivo aportar a la comunidad educativa de la aldea global una colección de recursos educativos interactivos que ayuden al aprendizaje de la Geografía mundial con diferentes niveles de detalle y con diferentes ámbitos disciplinarios, es decir, la Geografía general, física y humana, y la Geografía regional:

• Proyecto GEOcolor (colorea los países y estados del mundo)
• Proyecto GEOcapital (geolocaliza las capitales del mundo)
• Biblioteca GEOdiver (actividades lúdicas para aprender sobre continentes)
• Proyecto GEOevaluación (¿cuánto he aprendido?)

Red Descartes 2021/Año 1, núm. 2

Podemos acceder a todos los recursos del Proyecto GEOgráfica desde la siguiente imagen:

Además, recomendamos conocer y visitar los siguientes espacios:

• Empiezo 1º y 2º de Primaria
• Modelos didácticos para Primaria
• Procesos metodológicos y estrategias didácticas de éxito en Infantil y Primaria
• Aplicación de juegos didácticos en el aula
• Sudoku 4x4
• Sudoku 6x6

Finalmente, en la imagen siguiente, encontramos el acceso al catálogo completo y actualizado de recursos interactivos para primaria, accesibles desde cualquier dispositivo móvil, ordenador personal, portátil o pizarra digital.

Red Descartes 2021/Año 1, núm. 2

Educación Secundaria Obligatoria (entre 12 y 16 años)

En este artículo se presenta una guía de los diversos materiales interactivos que se pueden encontrar para la Educación Secundaria Obligatoria (ESO). Entre los diferentes proyectos encontramos unidades estructuradas como secuencias didácticas con actividades de introducción, desarrollo y evaluación de un tema concreto, pero también unidades aisladas para complementar, reforzar o ampliar los conceptos trabajados.

Red Descartes 2021/Año 1, núm. 2

El Proyecto "ED@D" (Educación Digital con Descartes) surge con el propósito de desarrollar recursos educativos digitales interactivos para la Educación Secundaria Obligatoria (ESO) en las áreas curriculares de Matemáticas, Biología y Física y Química, que permitan su uso tanto en la enseñanza presencial como en la formación a distancia. Las unidades del área de Matemáticas se encuentran disponibles en castellano, català, galego y, algunas unidades, en português.

Podemos acceder a todos los recursos del Proyecto ED@D desde la imagen inferior:

Ofrecemos numerosas Unidades Didácticas de Matemáticas y de Física y Química que han sido desarrolladas por profesores y profesoras y que recogen la experiencia adquirida en el aula. Presentan una estructura desagregada, es decir, son independientes unas de otras y ello permite que cualquiera pueda seleccionarlas, reorganizarlas y adaptarlas a sus necesidades y generar secuencias didácticas y planes educativos personalizados.

Red Descartes 2021/Año 1, núm. 2

Podemos acceder a todas las Unidades Didácticas, clasificadas por índices temáticos o niveles, desde la imagen inferior:

El Proyecto Miscelánea recoge escenas aisladas que tratan aspectos muy variados del currículo de Matemáticas y que pueden servir para que el profesorado las utilice directamente para ilustrar conceptos y técnicas básicas, o para que construya con ellas actividades y propuestas de trabajo en el aula. Pretende ser una caja de herramientas matemáticas que cada docente puede utilizar como apoyo y refuerzo al trabajo diario. El profesorado podrá disponer de escenas para diseñar sus propias lecciones, creando actividades para que el alumnado investigue, deduzca y llegue a conclusiones por sí mismo.

La secuenciación y programación didáctica personalizada, a partir de los bancos de recursos digitales existentes, requiere un tiempo del que no siempre se dispone.

Red Descartes 2021/Año 1, núm. 2

En este contexto, el subproyecto Miscelánea del proyecto Descartes, aporta un conjunto de materiales digitales interactivos que mantiene al profesorado en un entorno y rol que le es habitual, aportándole una necesaria y deseable transparencia e invisibilidad tecnológica, y consecuentemente facilitándole y permitiéndole una implemen- tación natural de las TIC.

Podemos acceder a todos los recursos del Proyecto Miscelánea desde la imagen inferior:

Para el tratamiento de los problemas en la materia de Física y Química ofrecemos una colección de enunciados que tratan aspectos muy diversos y que pueden servir para que el profesorado los utilice directamente para ilustrar los conceptos o construir con ellos actividades y propuestas de trabajo en el aula, disponiendo de materiales para que el alumnado investigue, deduzca y llegue a conclusiones por sí mismo.

Podemos acceder a los problemas de Física y Química para 4º ESO desde la imagen siguiente:

Red Descartes 2021/Año 1, núm. 2

Telesecundaria es una modalidad en el sistema educativo de México para la que se han elaborado numerosos materiales educativos que pueden consutarse vía web o bien pueden descargarse para su consulta en local. Estos recursos, para las materias de Matemáticas, Física y Química, tienen diferentes formatos (libros, audios, vídeos, tutoriales, interactivos, etc.) y contemplan como destinararios bien al alumnado, al profesorado o a ambos.

• Matemáticas 1º
• Matemáticas 2º
• Matemáticas 3º
• Física

Podemos acceder a todos los recursos del Proyecto Telesecundaria desde la imagen siguiente:

Red Descartes 2021/Año 1, núm. 2

Llega el momento para la materia troncal de Geografía e Historia con el Proyecto GEOgráfica, que tiene como objetivo aportar a la comunidad educativa de la aldea global una colección de recursos educativos interactivos que ayuden al aprendizaje de la Geografía mundial con diferentes niveles de detalle y con diferentes ámbitos disciplinarios, es decir, la Geografía general, física y humana, y la Geografía regional:

• Proyecto GEOcolor (colorea los países y estados del mundo)
• Proyecto GEOcapital (geolocaliza las capitales del mundo)
• Biblioteca GEOdiver (actividades lúdicas para aprender sobre continentes)
• Proyecto GEOevaluación (¿cuánto he aprendido?)

Podemos acceder a todos los recursos del Proyecto GEOgráfica desde la siguiente imagen:

Red Descartes 2021/Año 1, núm. 2

El Proyecto Competencias recoge objetos de aprendizaje interactivos cuyo objetivo es la formación y evaluación competencial. Sus contenidos se basan en las unidades liberadas de PISA y en las de las pruebas de evaluación de diagnóstico de diferentes comunidades autónomas españolas. Mientras las pruebas oficiales que se liberan son de carácter estático, y una vez resueltas caracen de interés para el alumnado, con Descartes se reconvierten y adquieren dinamismo e interactividad, permitiendo a sus usuarios la adquisición de competencias. Por tanto, pasamos de un recurso informativo a uno formativo y como complemento, si se desea, sigue sirviendo adicionalmente como un instrumento para la evaluación.

Podemos encontrar recursos para competencia matemática, comunicación lingüística en castellano, comunicación lingüística en inglés, conocimiento e interacción con el medio, social y ciudadana y competencias lectora y resolución de problemas.

En las siguientes imágenes proporcionamos los enlaces a estos objetos para cada curso:

Red Descartes 2021/Año 1, núm. 2

En 2015, la OCDE introdujo en su programa PISA la utilización del ordenador como herramienta para llevar a cabo el proceso de evaluación. Ello ha supuesto incorporar cambios en el procedimiento,

Red Descartes 2021/Año 1, núm. 2

pero el fundamental se manifiesta en el tipo de recursos para evaluar.

En el Proyecto PISA con ordenador podemos distinguir dos bloques o tipos de recursos, diferenciándose esencialmente en que unos tienen retroalimentación de las respuestas aportadas por el usuario me- diante impresión, descarga y/o envío por correo y otros que no tienen esta retroalimentación.

Podemos acceder a los recursos desde la siguiente imagen:

En la sección PISA 2017 (con algunos objetos diseñados para la modalidad de evaluación en papel y otros con ordenador), ofrecemos para la evaluación en 4º ESO materiales basados en las pruebas liberadas del programa PISA de:

Red Descartes 2021/Año 1, núm. 2

• Ciencias
• Comprensión lectora
• Finanzas
• Matemáticas
• Resolución de problemas

Podemos acceder a todos los recursos de PISA 2017 desde la imagen siguiente:

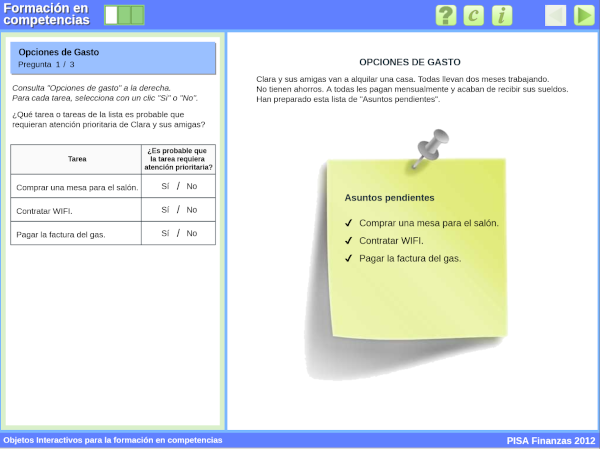
ASIPISA es una palabra palíndroma, acrónimo de “Ayuda Sistemática Interactiva para PISA”, que da nombre a un proyecto de desarrollo de materiales educativos, digitales e interactivos, basados en las

Red Descartes 2021/Año 1, núm. 2

unidades liberadas del Programa internacional PISA, pero introduciendo variabilidad mediante semillas aleatorias que dinamizan su contenido, evitan la repetición e incrementan su potencial instructivo. Todo ubicado en el contexto de las Tecnologías de la Información y de la Comunicación que incrementan la motivación y mejoran el aprendizaje competencial del alumnado.

Ofrecemos dos repositorios de objetos de aprendizaje, uno para el área competencial de Matemáticas y otro para el área de Lengua, Ciencias y Resolución de Problemas, a los que podemos acceder desde las siguientes imágenes:

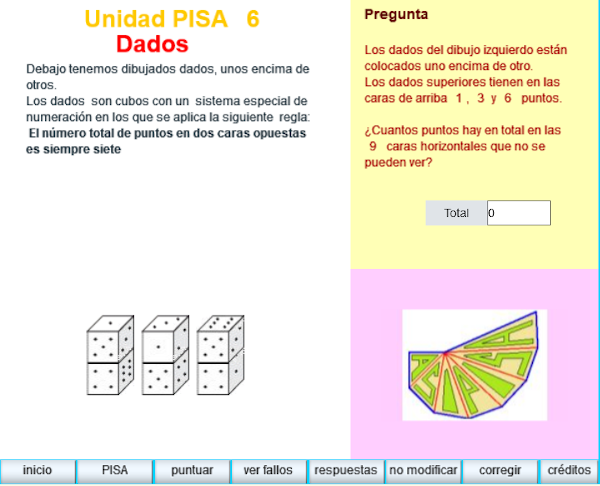
Red Descartes 2021/Año 1, núm. 2

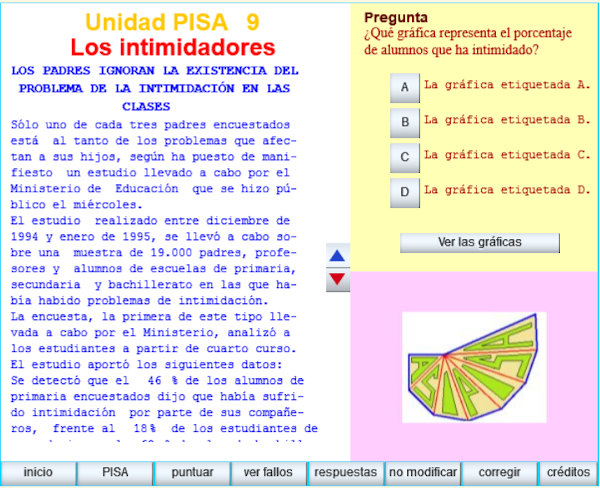
En el Taller de Matemáticas disponemos de 25 unidades variadas destinadas a servir en el curso homónimo de la Universidad Autónoma de México (UAM) Cuajimalpa. Los recursos se encuentran empaquetados según el estándar SCORM 1.2 y en la evaluación se presentan 5 preguntas de opción múltiple que comunican la calificación del alumnado a la plataforma Moodle utilizando el API del mismo estándar SCORM.

Se tratan temas fundamentales de aritmética, álgebra, trigonometría, geometría y geometría analítica, pudiendo acceder desde la imagen siguiente:

Red Descartes 2021/Año 1, núm. 2

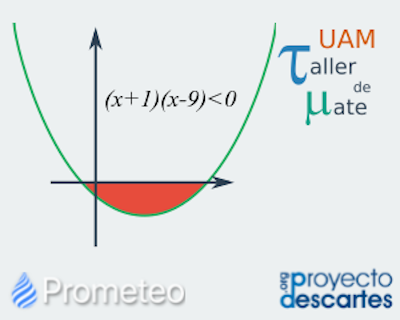
¿Idiomas con Descartes? Pues sí, disponemos de un pequeño y humilde repositorio con las preguntas de las pruebas propuestas en el primer Estudio Europeo de Competencia Lingüística, realizado en 2011, adaptadas como recursos interactivos TIC. En total son ocho en inglés y otras tantas en francés, de las que cuatro son de comprensión lectora y otras cuatro de comprensión oral, y constituyen un excelente instrumento didáctico para el aprendizaje de idiomas, en cualquiera de los cursos de la Educación Secundaria Obligatoria, aunque inicialmente fueran diseñados para su aplicación en 4º curso.

Podemos acceder a todos los recursos desde la siguiente imagen:

Red Descartes 2021/Año 1, núm. 2

Finalmente, en la imagen inferior, encontramos el acceso al catálogo completo y actualizado de recursos interactivos para ESO.

Red Descartes 2021/Año 1, núm. 2

Bachillerato (entre 16 y 18 años)

Para este nuevo curso académico 2021/2022 ofrecemos una amplia colección de objetos y libros dinámicos e interactivos de ayuda a la enseñanza y al aprendizaje de los contenidos curriculares de diferentes materias de Bachillerato (16 a 18 años). Así, en el proyecto Unidades Didácticas podemos encontrar las que han elaborado docentes a pie de aula, basadas en su experiencia, para las materias de Matemáticas y Física y Química.

Podemos acceder a todas las Unidades Didácticas, clasificadas por índices temáticos o niveles, desde la imagen inferior:

El Proyecto Miscelánea recoge escenas aisladas que tratan aspectos muy variados del currículo de Matemáticas y que pueden servir para que el profesorado las utilice directamente para ilustrar conceptos y técnicas básicas, o para que construya con ellas actividades y propuestas de trabajo en el aula, y que enlazamos en la siguiente página para cada uno de los cursos:

Red Descartes 2021/Año 1, núm. 2

• Recursos para Matemáticas - 1
• Recursos para Matemáticas - 2

Podemos acceder a todos los recursos del Proyecto Miscelánea desde la imagen inferior:

El Proyecto Un_100 recoge 101 unidades didácticas o recursos educativos de las áreas de Matemáticas y Física y son para el nivel de licenciatura o grado, aunque un número considerable también pueden ser usados en el bachillerato. En su elaboración han participado académicos de México, España, Colombia y Chile.

Se encuentran clasificados en 19 categorías temáticas a las que podemos acceder desde la siguiente imagen:

Red Descartes 2021/Año 1, núm. 2

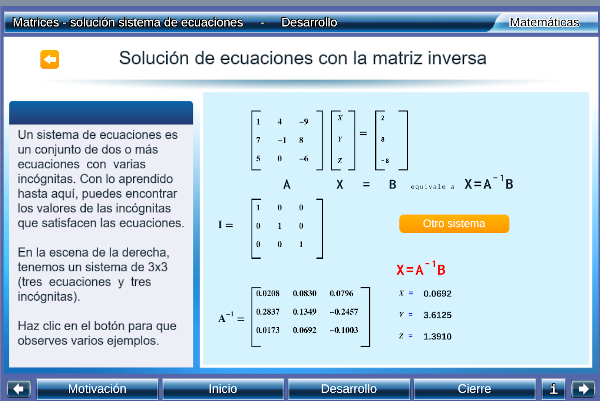
En Proyecto Newton presentamos enunciados de problemas que tratan aspectos muy diversos de Física y Química y que pueden servir para que el profesorado los utilice directamente para ilustrar los conceptos o para construir con ellos actividades y propuestas de trabajo en el aula para que el alumnado investigue, deduzca y llegue a conclusiones por sí mismo.

Enlazamos, seguidamente, a los problemas para cada curso de bachillerato:

• Problemas de Física y Química para 1º de Bachillerato
• Problemas de Física y Química para 2º de Bachillerato

Podemos acceder a todos los recursos del Proyecto Newton desde la imagen que figura en la próxima página:

Red Descartes 2021/Año 1, núm. 2

El Proyecto Prometeo está promovido por el Departamento de Educación del Instituto de Matemáticas de la UNAM (Universidad Nacional Autónoma de México) e incluye las unidades didácticas interactivas creadas por el Equipo Descartes. Las unidades consisten en una o varias escenas interactivas diseñadas para abordar temas principalmente de Matemáticas y Física, aunque también hay de otras materias.

Recomendamos los siguientes subproyectos:

• Recursos de Matemáticas para 1º de Bachillerato
• Recursos para el Taller de Matemáticas

Podemos acceder a todos los recursos del Proyecto Prometeo desde la imagen que figura a continuación:

Red Descartes 2021/Año 1, núm. 2

El Proyecto iCartesiLibri tiene como objetivo la conceptualización y el desarrollo de libros dinámicos, interactivos, multimedia, centrados en el aprendizaje y potenciadores de la educación de personas que aprenden a aprender, que adquieren autonomía y se forman competencialmente para afrontar su trayectoria vital.

MATEMÁTICAS 1º BACHILLERATO
Matemáticas básicas	Números complejos	Funciones trigonométricas
Análisis matemático	Cálculo diferencial	Geometría analítica

Red Descartes 2021/Año 1, núm. 2

Las cónicas	Trigonometría	Estadística

Nuestro diseño hace que estos libros sean accesibles y plenamente operativos en cualquier ordenador personal o en cualquier dispositivo móvil tipo tableta y smartphone, independientemente del sistema operativo que porte, ofreciendo un recubrimiento curricular para la materia de matemáticas en Bachillerato.

MATEMÁTICAS 2º BACHILLERATO
Álgebra lineal	Análisis matemático	Geometría analítica
Cálculo integral	Estadística	Álgebra lineal

Podemos acceder a todos los libros interativos del Proyecto iCartesiLibri desde la imagen que figura a continuación:

Red Descartes 2021/Año 1, núm. 2

Finalmente, en la imagen inferior, encontramos el acceso al catálogo completo y actualizado de recursos interactivos para Bachillerato.

Red Descartes 2021/Año 1, núm. 2

Universidad

El Proyecto Descartes ofrece gran cantidad de recursos interactivos y algunas descripciones de experiencias docentes que pueden aplicarse directamente en el aula universitaria o adaptarse para ajustarlo a nuestras necesidades. Con la presentación siguiente, se pretenden mostrar algunos de estos recursos y enlazar con páginas donde encontrar diversos tipos de materiales ya creados que pueden ser utilizados directamente o bien adaptarse con ayuda de la herramienta Descartes JS.

Destacamos el Proyecto iCartesiLibri, que se configura como una biblioteca de libros dinámicos, interactivos, multimedia, centrados en el aprendizaje y que facilitan la autonomía del alumnado.

Red Descartes 2021/Año 1, núm. 2

Ofrecemos en la siguiente distribución la biblioteca temática de libros interactivos de RED Descartes.

BIBLIOTECA TEMÁTICA DE LIBROS INTERACTIVOS
Artes visuales	Ciencias administrativas	Ciencias computacionales
Ciencias sociales	Física	Química
Ingeniería	Lengua inglesa	Formación en Descartes JS
Matemáticas	Literatura	Revista digital

Red Descartes 2021/Año 1, núm. 2

El Proyecto Miscelánea recoge escenas aisladas que tratan aspectos muy variados de Matemáticas y que pueden servir para ilustrar conceptos y técnicas básicas.

Podemos acceder a todos los recursos del Proyecto Miscelánea desde la imagen inferior:

El Proyecto Ingeniería y Tecnología tiene como objetivo ofrecer contenidos digitales que se encuadran en diferentes áreas de conocimiento y que en la mayoría de los currículos de programas de ingeniería o formación tecnológica se agrupan en cuatro apartados principales: ciencias básicas, ciencias de ingeniería, ciencias sociales y humanas, y aspectos o contenidos específicos de la profesión.

Así pues, aquí se abordan temas enmarcados en esos contextos y se dirigirán a diferentes disciplinas.

Red Descartes 2021/Año 1, núm. 2

Podemos acceder a todos los recursos del Proyecto Ingeniería y Tecnología desde la imagen inferior:

El Proyecto Un_100 recoge 101 unidades didácticas o recursos educativos de las áreas de Matemáticas y Física y en su elaboración han participado académicos de México, España, Colombia y Chile.

Se encuentran clasificados en 19 categorías temáticas a las que podemos acceder desde la imagen siguiente.

Red Descartes 2021/Año 1, núm. 2

¿Cómo buscar un recurso en el portal de Proyecto Descartes?

Red Descartes 2021/Año 1, núm. 2

Libros interactivos

Menú animado tomado de Mary Lou

Red Descartes 2021/Año 1, núm. 2

Números anteriores

Red Descartes 2021/Año 1, núm. 2

Guía para los autores

Características de los artículos

• El autor puede presentar el artículo en un documento de texto con un máximo de ocho paginas en Arial tamaño 12.
• Si el autor tiene competencias en el diseño HTML y CSS, puede usar la plantilla de la revista, con un máximo de 10 páginasPara este número se ha hecho la excepción con el artículo de "Difusión", pues presenta todos nuestros recursos digitales interactivos ofrecidos a la comunidad académica de la aldea global que, por la cantidad de recursos, no es posible reducirlo a un máximo de 10 páginas..
• El título será menor a 150 caracteres.
• Las imágenes, figuras, tablas, videos y objetos interactivos, se deben enviar en un archivo zip aparte.
• Idioma. La revista acepta artículos en español, inglés y portugués.
• Los artículos, preferiblemente, se relacionarán con aspectos educativos y el uso de las tecnologías en los procesos de enseñanza-aprendizaje. No obstante, se aceptan artículos de otras áreas del conocimiento, siempre que estos incorporen contenidos digitales diseñados con el editor DescartesJS.
• Presentar los permisos para el uso de contenido sujeto a derechos de autor, incluyendo los que provienen de Internet.

Red Descartes 2021/Año 1, núm. 2

El artículo y los anexos deben enviarse en una archivo zip, a través de un enlace (vía hosting o Google Drive, por ejemplo).

Los artículos deben abordar temas como:

• Difusión relacionada con la Red Educativa Digital Descartes
• Reseñas de libros interactivos
• Aplicaciones con DescartesJS
• Novedades DescartesJS
• Experiencias en el aula
• Investigaciones que incluyan el uso de contenidos digitales interactivos diseñados con DescartesJS

Evaluación de los artículos

El o los autores podrán sugerir revisores, indicando los datos de contacto (nombre y dirección de correo).

Los editores del Consejo Editorial, en primera instancia, valorarán los artículos para verificar que cumplen con los objetivos de publicación de la revista, si el concepto es positivo se asignarán mínimo dos revisores quienes evaluarán el artículo y harán las recomendaciones pertinentes, entre ellas la aceptación o no de su publicación.

Red Descartes 2021/Año 1, núm. 2