Número 1
Red Educativa Digital Descartes
Córdoba (España)
descartes@proyectodescartes.org
https://proyectodescartes.org
Revista Digital Red Descartes
https://proyectodescartes.org/iCartesiLibri/index.htm
ISSN: 2792-4483
Esta obra está bajo una licencia Creative Commons 4.0 internacional: Reconocimiento-No Comercial-Compartir Igual.
Algunos han sido extraídos de materiales publicados en el Proyecto Descartes, como materiales didácticos de diferentes subproyectos o como artículos del Blog Descartes y otros elaborados expre- samente para esta edición por colabo- radores de la organización RED Descar- tes.
Como se puede observar, la temática es muy diversa, aunque siempre relacionada con los objetivos del Proyecto Descartes y su herramienta homónima Descartes que permite generar escenas interac- tivas, sin excluir a ningún otro recurso, como soporte en el proceso de enseñan- za-aprendizaje en cualquiera de sus ámbitos científico, tecnológico, pedagó- gico, social, lingüístico-literario…
Esperamos que la revista se vaya mejo- rando con las sucesivas ediciones, acer- tando con la selección de temas en los nuevos artículos y contando siempre con las aportaciones y comentarios, que esperamos sean muchos, de nuestros lectores.
Ángel Cabezudo Bueno
Presidente
CSS
Colores CSS
Juan Guillermo Rivera Berrío
Introducción
En el diseño de contenidos digitales educativos se deben tener en cuenta algunos aspectos que, de entrada, hagan atractivo el contenido digital. Cuando se trata de objetos interactivos, como los desarrollados con DescartesJS, la in- teractividad per se lo hace bastante atractivo. No obstante, hay otros as- pectos adicionales que se deben con- siderar en el diseño del objeto, como lo es la intencionalidad pedagógica, que favo-
rece el aprendizaje y, el más descuidado de los aspectos, el "color" o, en general, la combinación de colores empleada en el objeto.
Detrás de algunos diseños, bastante atractivos, hay un equipo de profesionales, tales como pedagogos, diseñadores instruccionales, desarrolladores de software, diseñadores gráficos, animadores, y expertos temáticos, contratados para obtener contenidos digitales educativos, que cuentan con la financiación suficiente y, en muchos casos, la inversión se recupera, pues serán contenidos comerciales. Los cartesianos, desarrolladores de objetos interactivos, se caracte- rizan por su espíritu altruista, con poca o, generalmente, nula finan- ciación, por lo que tienen que hacer el papel de los profesionales citados anteriormente, lo que dificulta bastante su labor.
Red Descartes 2021/Año 1, núm. 1
Sin embargo, el trabajo en red, permite desarrollos colaborativos que, de alguna manera, suplen estas deficiencias, pues los miembros de la Red Educativa Digital Descartes se caracterizan por su diversidad geográfica y de formación, lo que permite la producción, también diversa, de contenidos digitales interactivos que satisfacen los currículos de diversos países, áreas de conocimiento y niveles de formación.
Pero, retornando al aspecto relacionado con el uso del "color", es apenas obvio que ante la ausencia de expertos en la "teoría del color", algunos diseños pierdan parte del atractivo obtenido con la interactividad.
Red Descartes 2021/Año 1, núm. 1
Los colores son capaces de establecer el tono adecuado para llevar el mensaje a los visitantes: pueden calmar, excitar, estimular a las acciones… (https://www.iempresa.net/creatividad/)
Dada la ausencia de formación en teoría del color, nuestros objetos, unidades y libros interactivos suelen incluir colores de acuerdo a los gustos del desarrollador y, como todos sabemos, los gustos también son diversos. Algunos incluyen excesivos colores que dispersan la atención del usuario, otros usan pocos colores que vuelven poco atractivo (a la vista) el contenido digital y, también usual, los inadecuados contrastes entre texto y fondo.
Este artículo es un pequeño aporte a corregir algunas de estas deficiencias de diseño.
Colores en DescartesJS
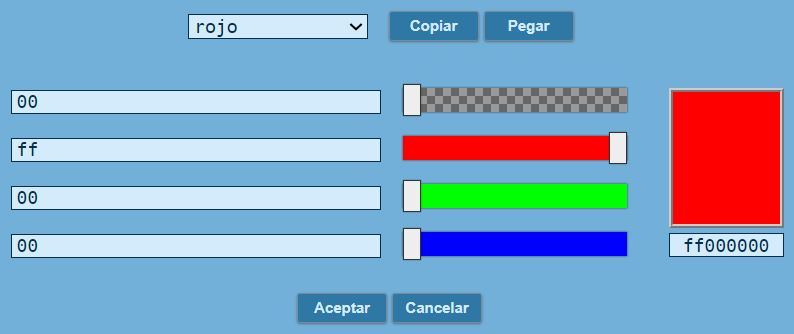
El editor DescartesJS permite seleccionar el color de los espacios, textos, controles y elementos tipo gráfico; para ello, presenta botones que al activarlos muestra un interactivo que permite escoger el color a utilizar (Figura 1).
Red Descartes 2021/Año 1, núm. 1
El menú superior cuenta con 13 colores a escoger: negro, magenta, azul, turquesa, verde, amarillo, naranja, rojo, rosa, gris oscuro, gris, gris claro y blanco. Pero, si ninguno de estos colores es el deseado, se puede hacer uso de las barras o los cuadros de texto para encontrar una combinación que se ajuste al gusto del diseñador.
En el siguiente interactivo, hemos emulado parte del suministrado por el editor DescartesJS, incluyendo un segundo menú para seleccionar otros 15 colores y, además, la posiblidad de copiar el código de colores CSS que explicamos a continuación.
Haz clic en el botón de la esquina superior derecha, para que interactúes en una ventana más grande. Selecciona un color básico o especial y luego mueve las barras para obtener el color que se acomode más a tu gusto.
Red Descartes 2021/Año 1, núm. 1
Colores CSS
Todo contenido digital, diseñado en HTML5, incluye algunos estilos que se codifican en el archivo html que lo ejecuta o, más recomendable, en un archivo externo generalmente llamado style.css. Este archivo se suele llamar hoja de estilos (Style Sheet) y por la forma como se dispone y aplica (estilos heredados en cascada) se suele denominar "Hojas de estilo en cascada" (Cascading Style Sheets) o CSSLa especificación CSS es mantenida por el World Wide Web Consortium (W3C). El MIME type text/css está registrado para su uso por CSS descrito en el RFC 2318.5. El W3C proporciona una herramienta de validación de CSS gratuita para los documentos CSS (https://es.wikipedia.org/)..
Los estilos permiten un cambio radical en la apariencia de un archivo html, pues modifican espacios (márgenes), tipos y tamaños de letra, dimensiones de párrafos e imágenes, fondos y coloresAl interactivo anterior, se le aplicó un estilo para el fondo, llamado "gradiente cónico", usando los colores red, yellow, lime, aqua, blue, magenta, red.. De estos últimos, los colores, nos ocuparemos a continuación.
Los códigos de color HTML, aprobados por el W3C, se obtienen de valores tipo Hex, RGB (decimal) o HSL. También, es posible identificar un color por su nombre, que para el W3C son 16 colores básicos (aqua, black, blue, fuchsia, gray, green, lime, maroon, navy, olive, purple, red, silver, teal, white, and yellow) escritos en inglés, de los cuales se desprenden más colores (coral, salmon, orange, gold, etc.).
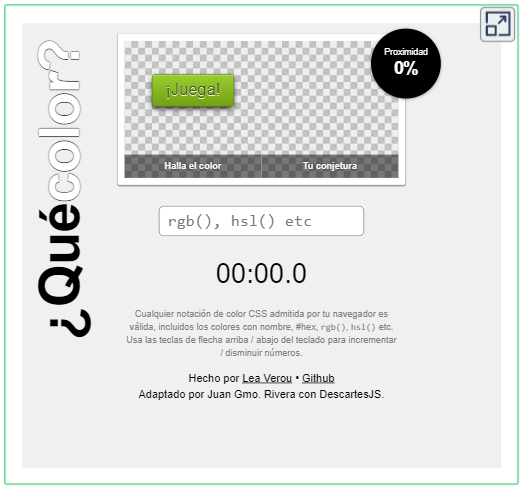
En el siguiente interactivo, diseñado por Lea Verou, haz clic en el botón CSS. Observarás que el fondo (background) de la ventana derecha es púrpura (purple), cambia este fondo con otros colores, usando los nombres anteriores o algunos que conozcas.
Red Descartes 2021/Año 1, núm. 1
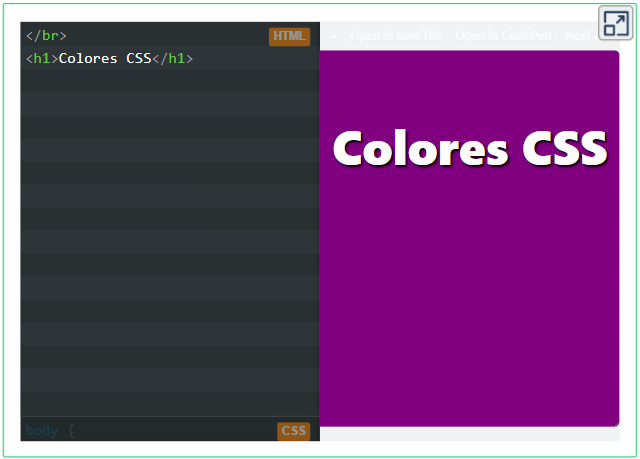
Colores RGB en valores hexadecimales (Hex)
En el formato RGB un color se identifica por la combinación de los colores rojo (Red), verde (Green) y azul (Blue), de allí el término RGB.
Un valor RGB en notación hexadecimal se expresa con un '#' seguido inmediatamente de seis caracteres hexadecimales; por ejemplo, #FF0000 representa al rojo, el cual se puede simplificar como #F00. Al disminuir los valores se obtendrán colores más oscuros; por, ejemplo, con #800000 se obtiene el color granate (maroon) que es un rojo más oscuro (pruébalo con el interactivo DescartesJS).
En el interactivo de Lea Verou, cambia el fondo usando valores hexadecimales; por ejemplo, el color granate: background: #800000.
Red Descartes 2021/Año 1, núm. 1
Los valores hexadecimales de los 16 colores básicos de la W3C se muestran en la siguiente imagen:
Colores RGB en valores decimales
En el formato hexadecimal, el valor máximo del rojo, verde o azul es $FF$, que en valor decimal es $255$, pues $FF = 15\times 16^1+15\times 16^0 = 255$. El formato de un valor RGB en la notación decimal o funcional es "rgb(" seguido de una lista separada por comas de tres valores numéricos (ya sea tres valores enteros o tres valores porcentuales) seguido de "). Para el caso del rojo, sería rgb(255,0,0) o rgb(100%,0%,0%), pruébalo con el editor de Lea Verou.
Red Descartes 2021/Año 1, núm. 1
Valores de color RGBA
El modelo de color RGB se amplía con un cuarto valor que permite la especificación de la opacidad del color, siendo uno (1) el máximo valor y cero (0) el mínimo u opacidad nula, que es lo mismo que transparencia máxima. Por ejemplo, el color rojo sería rgba(255,0,0,1) o rgb(100%,0%,0%,1). Usa el editor disminuyendo la opacidad, por ejemplo rgba(255,0,0,0.5).
Valores de color HSL
CSS incluye colores numéricos de matiz-saturación-luminosidad (HSL, por sus siglas en inglés) como complemento a los colores numéricos RGB. Este método es intuitivo, por contraste al RGB que no lo es. Una ventaja de HSL es que es simétrico a la claridad y la oscuridad.
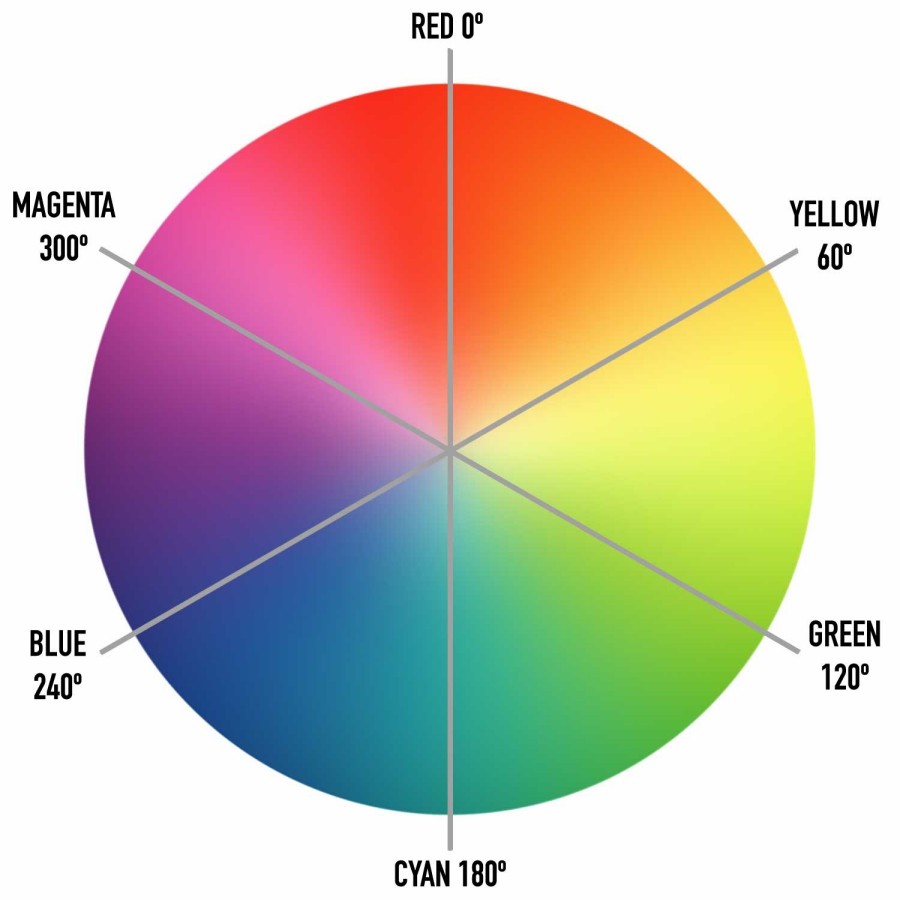
Los colores HSL se codifican como una tripleta (tono, saturación, luminosidad). El tono se representa como un ángulo del círculo cromático (Figura 3). Este ángulo se mide en grados. Por definición, rojo = 0 = 360, y los otros colores se distribuyen alrededor del círculo, por lo que el verde es igual a 120, el azul igual a 240, etc. Como ángulo, implícitamente se envuelve de tal manera que -120 = 240 y 480 = 120. La saturación y la luminosidad se representan como porcentajes, 100% es saturación total y 0% es un tono de gris. El 0% de luminosidad es negro, el 100% de luminosidad es blanco y el 50% de luminosidad es "normal", el rojo, entonces, sería hsl(0,100%,50%) o hsl(360,100%,50%).
El círculo cromático es una herramienta indispensable para diseñadores y artistas. Permite seleccionar colores de forma armoniosa. Consiste en 6 colores básicos (rojo, naranja, amarillo, verde, azul y violeta) y las mezclas entre los que se sitúan más próximos dentro del círculo (https://www.iempresa.net/creatividad/).
Red Descartes 2021/Año 1, núm. 1
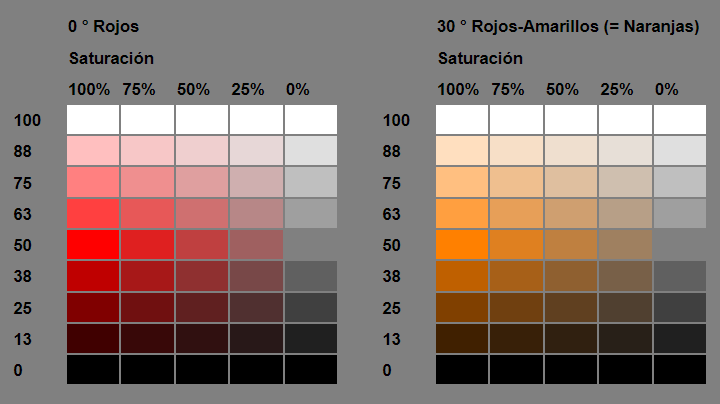
Finalmente, te proponemos los siguientes ejercicios. El primer ejercicio es usar el editor de Lea Verou para obtener los colores de la Figura 3 (el eje horizontal es la saturación y el vertical la luminosidad). El segundo ejercicio es un juego interactivo, también de Lea VerouLea Verou es una desarrolladora web, originaria de Lesbos, Grecia. Actualmente cursa un doctorado en Ciencias de la Computación en el MIT . Escribió un libro superventas sobre CSS avanzado que se ha traducido a 8 idiomas, trabajó en W3C y es una experta invitada en el W3C CSS Working Group , un honor que actualmente se extiende a solo 15 personas en todo el mundo., que consiste en hallar el código del color por su nombre o por formato hexadecimal, RGB o HSL, si practicas un buen tiempo, observarás que el HSL es el más adecuado para acertar los colores.
Red Descartes 2021/Año 1, núm. 1
Red Descartes 2021/Año 1, núm. 1
Combinaciones de colores
Como lo dijimos en la introducción, la combinación de colores es un aspecto clave a considerar. Una buena ayuda la da la página "Color Combos", que podemos explorar en https://www.colorcombos.com/, de la cual te presentamos el combo de colores 2:
Red Descartes 2021/Año 1, núm. 1
Libros interactivos
Recursos educa- tivos abiertos en portugués
José Antonio Salgueiro González
La Red Educativa Digital Descartes
RED Descartes es una asociación no gubernamental, sin ánimo de lucro, que tiene como fin promover la renovación y cambio metodológico en los procesos de aprendizaje y enseñanza de las Matemáticas, y también en otras áreas de conocimiento, utilizando los recursos digitales interactivos generados en el Proyecto Descartes.
Características de los recursos educativos abiertos
- Son de acceso gratuito a través de internet para docentes, alumnado y familias, así como para la formación de cualquier persona.
- Permiten la descarga de su archivo fuente para ser usado sin necesidad de conexión a internet, con la posibilidad de su modificación, adaptación y reutilización.
- Se publican con una licencia abierta, Creative Commons, para facilitar y posibilitar todo lo anterior.
Red Descartes 2021/Año 1, núm. 1
Livro Digital Interativo: Um exemplo em Trigonometria
Haz clic sobre la imagen para acceder al libro interactivo, que recomendamos visualizar maximizando la ventana.
Este livro foi realizado como TCC do mestrado profissional em matemática PROFMAT na Universidade Federal do Espírito Santo (UFES), Vitória (Espírito Santo), Brasil, por Eduardo Alejandro Flores Araya
Decidimos mostrar esta aplicação que não é conhecida no Brasil e que pode ajudar no processo de ensino-aprendizagem pela interatividade que ela apresenta.
Red Descartes 2021/Año 1, núm. 1
Declaración de París de 2012
El término Recursos Educativos Abiertos fue acuñado en el Foro de 2002 de la UNESCO, y designa a materiales de ense- ñanza, aprendizaje e investigación en cual- quier soporte, digital o de otro tipo, que sean de dominio público o que hayan sido publicados con una licencia abierta que permita el acceso gratuito a esos mate- riales, así como su uso, adaptación y re- distribución por otros sin ninguna res- tricción o con res- tricciones limitadas.
Ensino Fundamental II 6º ano (11 a 12 anos)
El profesorado, para poder incorporar las TIC en el proceso educativo, necesita disponer de recursos digitales que desarrollen los contenidos curriculares y que contemplen la actividad diaria, docente y discente, dentro y fuera del aula.
Haz clic sobre cada imagen para acceder a los libros interactivos.
Red Descartes 2021/Año 1, núm. 1
Matemática básica
Haz clic sobre la imagen para acceder al libro interactivo, que recomendamos visualizar maximizando la ventana.
Este livro é uma compilação de conteúdos e exercícios interativos de aritmética e álgebra básicas. Seu objetivo principal é possibilitar ao leitor revisar os conceitos elementares necessários à realização de cálculos numéricos com números reais, bem como a manipulação de expressões algébricas, radicais, racionais e polinômios em geral.
Red Descartes 2021/Año 1, núm. 1
ODS4
Desde la ONG RED Descartes, trabajamos de forma altruista para colaborar y apoyar los Objetivos de Desarrollo Sostenible de la UNESCO, y muy espe- cialmente el denomina- do ODS4, cuyo fin es garantizar una educa- ción inclusiva, equita- tiva y de calidad y promover oportunida- des de aprendizaje durante toda la vida para todos.
El 25 de septiembre de 2015, los líderes mundiales adoptaron un conjunto de objetivos globales para erradicar la pobreza, proteger el planeta y asegurar la prosperidad para todos como parte de una nueva agenda de desarrollo sostenible.
Ensino Fundamental 2º ano
Este livro tem dois objetivos. Por um lado, permite que o aluno do segundo ano do Ensino Fundamental aprenda e pratique a soma de números naturais e, por outro lado, sirva de exemplo para os professores de como um livro interativo pode ser desenvolvido utilizando cenas produzidas no DescartesJS onde o livro interativo adota um formato que simula um livro clássico.
Haz clic sobre la imagen para acceder al libro interactivo, que recomenda- mos visualizar maximizando la ven- tana.
Red Descartes 2021/Año 1, núm. 1
Por que gosto de Descartes?
Comunidad de Países de Lengua Portuguesa
Según Wikipedia, 223 millones de personas en el mundo hablan la lengua portuguesa, distribuidas en países de varios continentes y constituyendo la Comunidad de Países de Lengua Portuguesa, integrada por Angola, Brasil, Cabo Verde, Guinea-Bissau, Guinea Ecuatorial, Mozambique, Santo Tomé y Príncipe, Portugal y Timor Oriental.
Desde RED Descartes hemos comenzado a traducir nuestros recursos educativos abiertos a portugués de Brasil, gracias a la inestimable colaboración del profesor Lindberg Barbosa Lira de Almeida.
Red Descartes 2021/Año 1, núm. 1
Subtração
Haz clic sobre la imagen para acceder al libro interactivo, que recomendamos visualizar maximizando la ventana.
Neste livro, trabalhamos "Subtração" por meio de cenas interativas com autocorreção que contribuem para a aprendizagem autônoma ou orientada pelo professor. É direcionado aos alunos do segundo ano do ensino fundamental ou do terceiro ano como revisão. No algoritmo da subtração, o critério tradicional foi aplicado para "transportar", ou seja, quando o número do subtraendo é maior que o do minuendo, o número transportado é adicionado ao próximo número do subtraendo.
Red Descartes 2021/Año 1, núm. 1
Números Inteiros. Adição e subtração
Haz clic sobre la imagen para acceder al libro interactivo, que recomendamos visualizar maximizando la ventana.
Este livro é um breve resumo a respeito de tais operações que permite o aprendizado e a prática de somar e subtrair números inteiros por meio de exercícios interativos que podem ser repetidos, com dados diferentes, quantas vezes se deseje sendo corrigidos automaticamente. Isso dá autonomia ao estudante e o permite avançar com ou sem o apoio direto de um professor.
Red Descartes 2021/Año 1, núm. 1
Números Inteiros. Multiplicação e divisão
Haz clic sobre la imagen para acceder al libro interactivo, que recomendamos visualizar maximizando la ventana.
Este livro permite o aprendizado e a prática da multiplicação, divisão, potenciação e expressões numéricas com números inteiros por meio de exercícios interativos que podem ser repetidos, com dados diferentes, quantas vezes quiser e que são corrigidos automaticamente. Usado como uma ferramenta de aprendizagem autônoma ou como um reforço do trabalho realizado em sala de aula.
Red Descartes 2021/Año 1, núm. 1
Frações
Haz clic sobre la imagen para acceder al libro interactivo, que recomendamos visualizar maximizando la ventana.
Este livro permite o aprendizado e a prática das frações e suas operações. São utilizados textos curtos, focando o aluno na realização de exercícios interativos com autocorreção e explicações dirigidas. Este livro contribui para a aprendizagem autônoma e, ao mesmo tempo, serve como um suporte ao trabalho docente.
Red Descartes 2021/Año 1, núm. 1
Investigación
Artículo publicado en la revista Epsilon de la SAEM Thales
Ángel Cabezudo Bueno
En el número 106 de la revista Epsilon de la Sociedad Andalu-
za de Educación Matemática Thales se ha publicado el artículo titulado "Congruencias en el triángulo de Pascal y el rectángulo de Newton" cuyo autor es nuestro socio José R. Galo Sánchez. Un trabajo de investigación, que como se re- fleja en la filiación de la autoría, ha sido desarrollado dentro de nuestra RED Descartes.
Este trabajo fue prepublicado en nuestro blog en tres artículos en los que el autor divulgaba la investigación realizada:
- El paralelogramo de Newton el 6 de marzo de 2020.
- El rectángulo de Newton como "simétrico" del triángulo de Pascal el 27 de marzo de 2020.
- Congruencias en el triángulo de Pascal el 24 de abril de 2020.
y, posterioriormente compiló el artículo que sometido a revisión por pares se ha publicado en la revista indicada.
Red Descartes 2021/Año 1, núm. 1
En el resumen se indica :
"El rectángulo de Newton surge como extensión del actualmente denominado triángulo de Pascal partiendo de la versión escalonada de Stifel. Sin embargo, si se parte del esquema organizativo aportado por Pascal entonces el rectángulo de Newton se obtiene mediante una simple simetría signada. Así pues, basta estudiar las congruencias con cero de los números combinatorios y en su análisis aportamos que éstas se ubican en una sucesión de triángulos básicos que se distribuyen de manera periódica. En base a esa periodicidad se incluye un criterio que permite determinar directamente la congruencia de un número combinatorio."
El plantemiento conceptual que sigue, puede sintetizarse en:
- Presentación del conocido triángulo de Pascal en su representación actual como triángulo isósceles escalonado y como triángulo rectángulo que es la original de Pascal, y presentación del menos divulgado rectángulo de Newton.
- Reducción del rectángulo de Newton al de Pascal mediante una simetría signada.
- Muestra de las congruencias con cero en el triángulo de Pascal y revisión de resultados previos de otros autores. Esos resultados se presentan normalmente de manera algebraica y, en general, son oscuros y difíciles de interpretar por profanos dada la abstracción que suele introducir el Álgebra, pero aquí son visualizados geométricamente quedando mostrados de manera diáfana tanto para legos como para ilustrados.
- Finalmente se enuncian algebraicamente los resultados obtenidos por el autor, los cuales muestran la periodicidad de las congruencias módulo p de los números combinatorios y la regla que permite su determinación directa a partir de la descomposición p-ádica del índice superior e inferior, y se visualiza el porqué de ese resultado.
Red Descartes 2021/Año 1, núm. 1
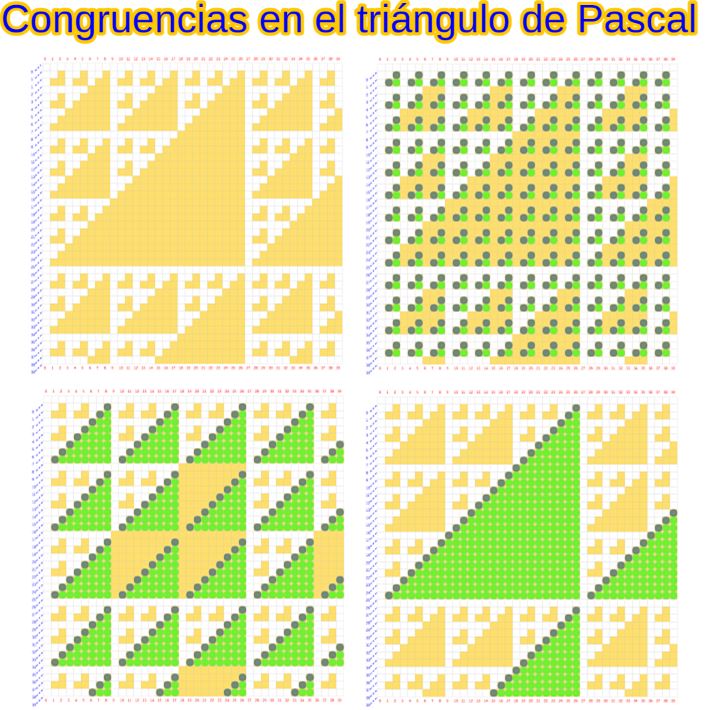Todo está aderezado por numerosas escenas interactivas que permiten al interesado reproducir la investigación y cómo, apoyándose en ellas, puede potenciarse la reflexión que permite alcanzar la meta lograda.
¡Acceda pulsando sobre la imagen!
Os incluimos a continuación dicho artículo y os invitamos a su lectura, a que realicéis observaciones y comentarios al mismo y a que lo divulguéis a través de vuestras redes sociales y profesionales.
También a que, usando los recursos interactivos ahí enlazados y disponibles en nuestra web, abordéis actividades en vuestra aulas en las que divulgar el Triángulo de Pascal, el rectángulo de Newton y las curiosas congruencias que acontecen en ellos y a la vez que podáis promover en vuestro alumnado la inquietud básica, la chispa a partir de la cual se cataliza la vocación investigadora.
Red Descartes 2021/Año 1, núm. 1
Red Descartes 2021/Año 1, núm. 1
Matemáticas
Expresiones mate- máticas con $\KaTeX$
Juan Guillermo Rivera Berrío
Introducción
El nuevo modelo de libro interactivo de la Red Educativa Digital Descartes incorpora la librería $\KaTeX$ que, según sus autores, es la biblioteca de composición tipográfica mate- mática más rápida de la web. Esta librería se basa en el sistema tipográfico $\TeX$ de Donald Knuth$\TeX$ se considera generalmente la mejor forma de componer fórmulas matemáticas complejas pero, especialmente en la forma de $\LaTeX$ (es.wikipedia.org/)..En el diseño de contenidos web es común usar imágenes o, eventualmente, librerías exter- nas tipo MathJax para incluir las expresiones matemáticas. Ya no será necesario recurrir a estas prácticas dispendiosas, pues basta usar los comandos tradicionales de $\LaTeX$ para escribir estas expresiones.
Dado que es compatible en un alto porcentaje con $\LaTeX$, no será problema para aquellos docentes que han hecho tra- bajos usando este sistema. Los ejemplos que explicaremos en este artículo, se encuentran en el libro "Diseño de libros in- teractivos", publicado en la Red Educativa Digital Descartes.
Usando $\KaTeX$
Para mostrar fórmulas mate- máticas se utiliza la biblioteca $\KaTeX$, la cual permite utilizar notación de $\LaTeX$ para repre- sentarlas dentro del código HTML. Por ejemplo, la siguiente expresión:\frac{\sqrt{b^2-4ac}}{2a}reproduce:
$$\frac{\sqrt{b^2-4ac}}{2a}$$
Red Descartes 2021/Año 1, núm. 1
$\KaTeX$ fue creado en 2014 por Emily Eisenberg y Sophie Alpert, mientras trabajaban en Khan Academy, quizá por ello el nombre: KA (Khan Academy) $\TeX$
Red Descartes 2021/Año 1, núm. 1
Como se observa en el video anterior, basta con usar comandos sencillos como \frac que significa "fraction" o fracción. En el siguiente interactivo, se pueden practicar algunos comandos. En la primera ventana (fondo negro), escribe \frac32:
¡Sencillo! ¿verdad? Ahora escribe \frac{x+1}{x^2-1}. Las llaves son necesarias cuando los argumentos (numerador y denominador) no son simples. Otro comando sencillo es \sqrt, que significa "SQuare RooT" o raíz cuadrada, prueba con \sqrt{b^2-4ac}.
Si se quiere escribir una integral, usamos el comando \int, para el límite inferior se usa el guión bajo y el superior con el circunflejo "^". Prueba con \int_{x=1}^{x=5}(x^3-1)dx (puedes hacer un copie y pegue de la expresión).
Red Descartes 2021/Año 1, núm. 1
Otras expresiones matemáticas
$\KaTeX$ permite escribir cual- quier tipo de expresión mate- mática.Vectores:
\vec{A} \space \hat{r}Conjuntos:
\forall x \in \varnothing \subseteq A \cap B\cup\existsLógica:
p \land \bar{q} \to p\lor \lnot qEs importante respetar los es- pacios, pues de no hacerlo el comando sería mal intepretado.
Red Descartes 2021/Año 1, núm. 1
Geometría: \triangle \angle \perp \| 45^\circ
Sumatorio: \sum_{k=1}^N k^2
Límite: \lim_{x \to{+}\infty}{f(x)}
Una ecuación alineada y con texto en color azul, la podemos escribir con el siguiente código: \color{blue}\begin{aligned}(a+b)^2 &= (a+b)(a+b)\\&= a^2 + ab + ba + b^2 \\&= a^2 + 2ab + b^2\end{aligned}
Observa que hemos usado dos barras inclinadas (\\), para el salto de línea.
Expresiones químicas
Finalmente, $\KaTeX$ incorpora una librería de JavaScript para la escritura de expresiones químicas, para lo cual hay que usar el comando \ce. Usa el interactivo, para escribir las siguientes expresiones:
\ce{CO2 + C -> 2 CO}
\ce{CH4 + 2O2 -> CO2 + 2H2O}
\ce{C6H5-CHO} \qquad \ce{A-B=C#D}
\ce{SO4^2- + Ba^2+ -> BaSO4 v}
Una lista completa de las funciones soportadas por $\KaTeX$ se encuentra en la siguiente dirección Funciones soportadas.
Red Descartes 2021/Año 1, núm. 1
¿Cómo se hizo?
Números aleatorios diferentes en juegos
Jesús Manuel Muñoz Calle
En este artículo presentamos cómo obtener varios números aleatorios diferentes para los juegos del Proyecto AJDA desde el punto de vista de su código DescartesJS. Esta opción es muy utilizada en los juegos, como por ejemplo para: que las preguntas que se hacen a los participantes sean diferentes y aleatorias, obtener diferentes cartas de una baraja, obtener diferentes fichas de dominó, seleccionar diferentes participantes para realizar una acción en un suelo, etc.
En primer lugar se crea un vector vacío, cuya dimensión sea la del número aleatorio máximo que se puede obtener (se puede indicar un número o dejarlo como parámetro). En este ejemplo llamaremos al vector valores2.
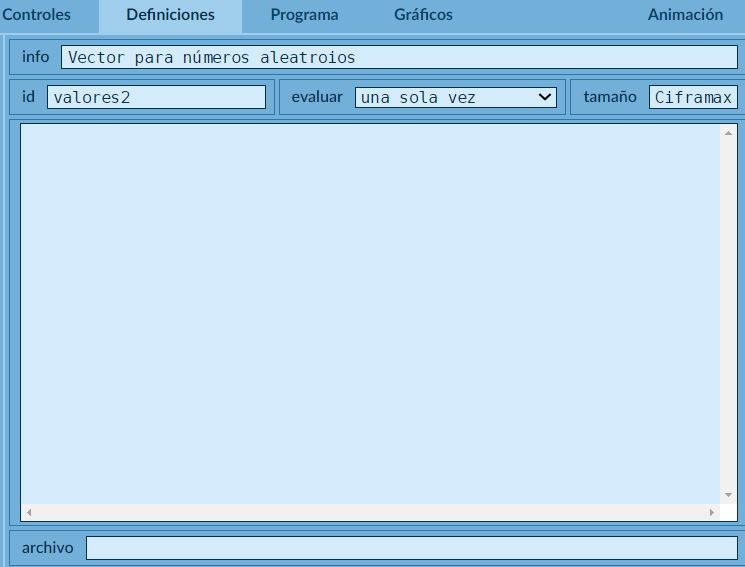
Red Descartes 2021/Año 1, núm. 1
Se crea un algoritmo (que hemos llamado iniciaValores2()) que rellena cada una de las filas del vector creado anteriormente desde uno hasta la cifra máxima del número aleatorio, tal y como se indica a continuaciónEl algoritmo original va de cero a la cifra máxima (ver artículo original)..
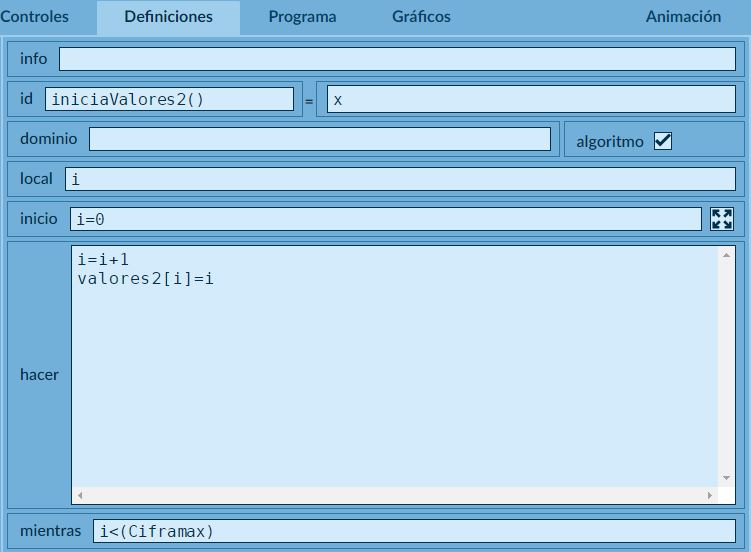
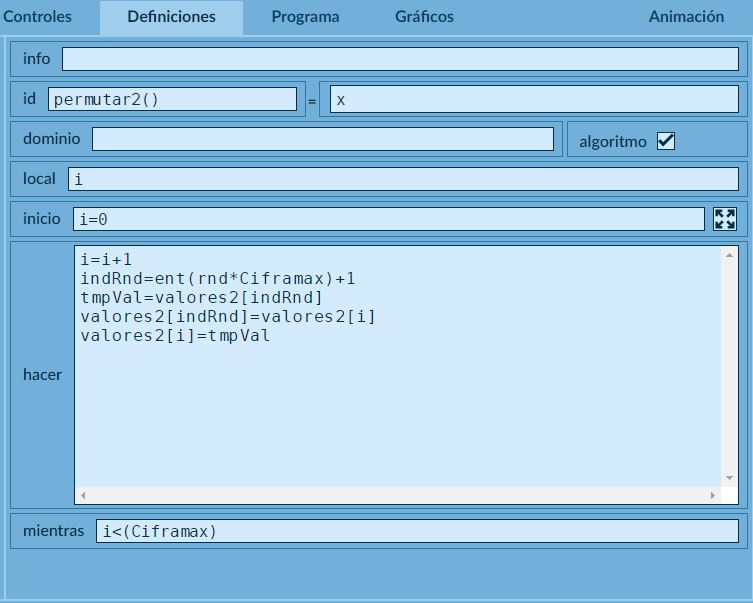
Se genera un nuevo algoritmo (que hemos denominado permutar2()) que asigna a cada fila un valor entre uno y la cifra máxima pero con una reordenación aleatoria.
Red Descartes 2021/Año 1, núm. 1
Comentamos el funcionamiento del algoritmo: se van a ir recorriendo las distintas filas del vector valores2 por orden secuencial (desde uno a la Ciframax) y en cada ciclo primero se obtiene un numero aleatorio entre uno y la cifra máxima, después se extrae el valor de la fila del vector dado por ese número aleatorio, a la fila extraída aleatoriamente se le da el valor de la fila que le corresponde por orden secuencial de la iteración y a ésta el valor de la fila sacada aleatoriamente. De esta forma en cada iteración se van permutando los números de las filas del vector de forma que tenemos un vector con un número aleatorio diferente en cada fila.
Red Descartes 2021/Año 1, núm. 1
Cuando invoquemos los dos algoritmos creados (iniciaValores2() y permutar2()) tendremos un vector (valores2) cuyas filas contienen números diferentes y con valores aleatorios entre uno y la cifra máxima que podremos utilizar cuando necesitemos.
Veamos un ejemploEste ejemplo es una adición de los editores de la revista.. En el siguiente interactivo, ingresa una cifra máxima entre 2 y 15.
Escribe, por ejemplo, 10 y presionas la tecla "Intro" varias veces. Observa cómo se generan diferentes asignaciones a los elementos del vector valores2.
Red Descartes 2021/Año 1, núm. 1
DescartesJS
Diseño de una calculadora estándar con DescartesJS
Juan Guillermo Rivera Berrío
Calculadora estándar
La primera calculadora electrónica surge en 1961, usando tubos de vacío: "Bell Punch Co., Uxbridge, Inglaterra, anunció las primeras calculadoras de escritorio electrónicas del mundo: la Anita Mk VIILa calculadora Anita (A New Inspiration To Arithmetic/Accounting) Mk VII se comercializó fuera de Gran Bretaña y la Mk VIII para los usuarios británicos, con gran aceptación por ser silenciosa y rápida." http://www.vintagecalculators.com/). Un año después, la compañía Philips presenta un prototipo de calculadora de escritorio de transistores de 3 funciones (sin división), que en 1963 y 1964 se comercializan con las cuatro operaciones básicas, destacándose la calculadora Sharp CS10A, con precios exorbitantes.
En 1969, surge la calculadora electrónica de mano Sharp QT-8B, que funciona con baterías. En 1973 se implementa el uso de pantallas LCD (dispositivo de cristal líquido), que reemplazan las de tipo LED (diodo emisor de luz). En 1976 aparecen las calculadoras con células solares.
La primera calculadora electrónica auténticamente de bolsillo fue la Busicom LE-120A HANDY, comercializada a principios de 1971 (https://es.wikipedia.org/wiki/Calculadora)
Este artículo está dedicado a las calculadoras estándar de bolsillo, ampliamente utilizadas por los estudiantes de los primeros niveles de formación.
Red Descartes 2021/Año 1, núm. 1
Se define una calculadora estándar como aquella que permite realizar cálculos aritméticos con las cuatro operaciones básicas (suma, resta, multiplicación y división). Cada modelo de calculadora estándar ofrece algunas operaciones complementarias, tales como la raíz cuadrada, porcentaje, cambio de signo y, actualmente, teclas para almacenar resultados (memoria). En la siguiente imagen animada, se observan modelos antiguos como la Handy Busicom y modelos actuales de empresas como Casio y Canon.
Calculadora estándar con DescartesJS
El objetivo de este artículo es mostrar cómo el editor DescartesJS permite diseñar una calculadora estándar, en la cual se han incorporado las operaciones básicas, la raíz cuadrada, el cálculo de porcentaje, el cambio de signo, memorias positiva, negativa y resultante, además del borrado parcial de datos, tal como se observa en el interactivo de la próxima página.
Red Descartes 2021/Año 1, núm. 1
Interactúa realizando operaciones con la calculadora:
El modelo, para quien ya ha diseñado escenas interactivas en DescartesJS, permite el cambio de la imagen de la calculadora, tal como se hizo en el libro Calculadoras electrónicas, publicado en la Red Educativa Digital Decartes.
Red Descartes 2021/Año 1, núm. 1
Haz clic en alguna de las siguiente imágenes, para que observes e interactúes con diferentes modelos de calculadoras estándar diseñadas con descartesJS:
 |  |  |
Algunas mejoras incluidas tienen que ver con posibles errores de interacción; por ejemplo, al presionar la tecla +, queda la duda si fue presionada, por ello se optó por incluirle sonido. En el modelo TREFOIL de la página anterior, se incluyó un botón para cambiar el color de la calculadora, de manera que cada persona pueda seleccionar el que le resulte más agradable.
No todas las calculadoras estándar ofrecen la posibilidad de repetir la última operación, presionando varias veces la tecla "=", lo que algunos llaman "factor constante", que resulta de presionar varias veces la tecla igual o un operador, así:
$7+12 ===$ dá como resultado $7+12+12+12= 43$, resultado que también se obtiene así
$7+12 ++ = 43$. Factor constante que también se puede usar con otros operadores.
Red Descartes 2021/Año 1, núm. 1
Cambio de imagen de calculadora
Dado que las calculadoras estándar actuales presentan, en general, las mismas operaciones básicas y complementarias, es posible cambiar la imagen del modelo TREFOIL por la de otra calculadora. Sólo tienes que cambiar la imagen, el tamaño de la escena, modificar la posición y tamaño de controles tipo botón y, finalmente, la posición de los gráficos tipo texto.
En el siguiente video mostramos algunos de estos cambios, realizados con el editor DescartesJS que, para un cartesiano, resultaría bastante sencillo. Ahora, si no sabes diseñar escenas interactivas con esta herramienta de autor, puedes optar por seleccionar algunas de las presentadas en el libro Calculadoras electrónicas e incorporarla en una página web, libro interactivo o cualquier otro contenido digital que estés desarrollando.
En el vídeo de la siguiente página, se calcula $\frac17 + \frac38$ directamente y, también, usando las memorias de la calculadora.
Red Descartes 2021/Año 1, núm. 1
Red Descartes 2021/Año 1, núm. 1
Difusión
René Descartes - El proyecto y la Red Educativa Descartes
Jesús Ignacio Calle Pérez y José R. Galo Sánchez
René Descartes
René Descartes (Renatus Cartesius: forma latinizada) fue un matemático, físico y filósofo nacido el 31 de marzo de 1596 (siglo XVI) en La Haye en Touraine (hoy conocida como Descartes en su honor)
y murió el 11 de febrero de 1650 (siglo XVII) de neumonía en Estocolmo (Suecia)La imagen es una pintura realizada por Alejandra Calle, hija del autor de este artículo.. Pertenecía a una familia de baja nobleza y su madre falleció al año de su nacimiento. René Descartes se destacó muy pronto en la escuela por sus capacidades intelectuales.
Se formó en las principales ramas del conocimiento clásico en el colegio jesuita Henri IV de La Flèche y a sus 18 años se decidió por estudiar Derecho en la Universidad de Poitiers (Poitiers-Francia). De los 22 a los 24 años estuvo en el ejército. Apenas renunció del ejército se dedicó a viajar por diferentes países de Europa como Dinamarca, los Países Bajos, Italia y Alemania, donde comenzaría a cultivar sus teorías científicas y filosóficas, gracias al contacto que tenía con grandes intelectuales de la época.
Red Descartes 2021/Año 1, núm. 1
En 1628 se radicó en los Países Bajos, donde se dedicó de lleno al estudio de la geometría, la lógica, la óptica y la filosofía. En esa época produce sus principales obras, entre las que sobresale el “Discurso del Método” (1637) donde está su declaración más conocida “Pienso, luego existo”, que en latín se expresa como “Cogito ergo sum”.
Fue considerado el padre de la geometría analítica (puente entre el álgebra y la geometría, usada en el descubrimiento del cálculo infinitesimal) y la filosofía moderna, así como uno de los principales protagonistas de la revolución científica. Descartes planteó las bases para el racionalismo moderno del siglo XVII, más tarde defendido por Spinoza, Malebranche y Leibniz, contraria a la escuela empirista inglesa compuesta por Hobbes, Locke, Berkeley y Hume.
El nombre de sistema de coordenadas cartesianas se le atribuye a él. Descartes también hizo contribuciones al campo de la óptica. Mostró utilizando la construcción geométrica y la ley de refracción que el radio angular de un arco iris es de 42 grados.
Red Descartes 2021/Año 1, núm. 1
El proyecto y la red educativa Descartes
Antes de conceptuar sobre el proyecto y la red educativa Descartes se definirán una serie de términos que hacen parte de dichos conceptos.
El applet Descartes en Java es obsoleto
Se consideró una herramienta de autor que permitía elaborar recursos didácticos interactivos que se embeben en páginas HTML. Los recursos elaborados con Descartes tienden a parecer imágenes animadas o animaciones, pero su esencia se centra en la interactividad (https://proyectodescartes.org/). No es lo mismo ver una película (animación) que ser actor en ella (interactividad).Red Descartes 2021/Año 1, núm. 1
DescartesJS es un intérprete actualizado de Descartes desarrollado en JavaScript que es compatible con el estándar HTML5 y, por tanto, es ejecutable en cualquier sistema operativo, dispositivo y/o navegador que cumpla dicho estándar (https://proyectodescartes.org/descartesjs).
Con DescartesJS se pueden desarrollar recursos educativos interactivos no solo en el ámbito de las matemáticas, área en la que comienza, sino en cualquier área de conocimiento científico o literario.
El Proyecto Descartes inició a mediados del año 1998, como un proyecto educativo del Ministerio de Educación de España que surge ligado a la herramienta de autor Descartes, pero también apoyada en diversos proyectos educativos que promovían el uso de las Tecnologías de la Información y de la Comunicación (TIC) en la educación.
Su objetivo principal es promover nuevas formas de enseñanza y aprendizaje 
de la Matemática integrando las tecnologías antes mencionadas en el aula como herramienta didáctica. Este proyecto ha ido evolucionando y ampliando su alcance a otras áreas científicas, sociales y literarias.
La Red educativa digital Descartes (Red Descartes) es una asociación no gubernamental, sin ánimo de lucro, constituida el 1 de junio de 2013, cuyo fin es promover la renovación y cambio metodológico en los procesos de aprendizaje y enseñanza de las Matemáticas y en otras áreas de conocimiento, utilizando los recursos digitales interactivos generados en el Proyecto Descartes mediante el desarrollo y difusión de la herramienta Descartes anteriormente descrita.
Red Descartes 2021/Año 1, núm. 1
Los socios y colaboradores de la Red Descartes son en su gran mayoría profesores de diferentes áreas académicas y niveles educativos.
En los estatutos de la asociación se detallan sus objetivos y la organización interna. El órgano de coordinación es la Junta Directiva. Su lema:
Entendiéndose el altruismo como la tendencia a procurar el bien de las personas de manera desinteresada, incluso a costa del interés propio.
En Colombia se constituyó la asociación homónima y hermana “Red Educativa Digital Descartes Colombia”.
Red Descartes 2021/Año 1, núm. 1
Pedagogía
Tecnopedagogía del modelo TPACK con DescartesJS
John Jairo García Mora
Planificar la enseñanza tiene como punto de partida el concepto de aprender: un conjunto resultado de la unión de rasgos cognoscitivos, afectivos y funcionales que muestra los indicadores de las posibles maneras de percibir los seres humanos, sus acciones al interactuar y cómo responden a sus ambientes de aprendizaje.
Esa planificación se denomina diseño instruccional y tiene como objetivo llevar un conocimiento organizado a grandes volúmenes de personas. Partiendo de esa meta a lograr, la historia nos remonta a la época de la segunda guerra mundial donde se elaboró gran cantidad de material de entrenamiento masivo para militares, pues debían adquirir rápidamente conocimientos bélicos para enfrentar al enemigo.
Ese incipiente diseño ins- truccional ha evolucionado desde el Conductismo de los años 60, la Teoría de Sistemas de los años 70, el Cognitivismo en los 80, el Constructivismo de los 90, hasta llegar al año 2004 cuando George Siemens y Stephen Downes presentan el Conectivismo: una teoría del aprendizaje para la era digital basada en el análisis de las limitaciones del Constructivismo, el Cognitivismo y el Conductismo, para explicar el efecto que la tecnología ha tenido sobre la manera en que actualmente vivimos, nos comunicamos y aprendemos.
Para crear una escena de DescartesJS que nos permita trabajar bajo el modelo tecnopedagógico TPACK es necesario conocer las características del diseño instruccional de Colvin (2008) bajo las cuales se realiza la escena interactiva:
- Despertar el interés o motivación del estudiante hacia el tema a tratar.
- La escena debe enfocarse en los elementos esenciales del tema a considerar, sin saturarla de contenido.
Red Descartes 2021/Año 1, núm. 1
- Debe incluir la activación de los conocimientos previos, haciendo uso de ventanas emergentes.
- Ajustar la instrucción a objetivos metacognitivos.
- Diseñar contenido signifi- cativo que promueva la memoria a largo plazo del estudiante.
- Construir modelos mentales robustos.
Transitar de un quehacer de aula centrado en el conocimiento a una labor adaptada al mundo digital, donde se privilegie el desempeño, en la que no solo los conocimientos sean valiosos, sino también los procesos y la vinculación con la realidad, se ha convertido en una de las nuevas tendencias en pedagogía y se denomina aprendizaje híbrido o Blended Learning (B-Learning). Surgido a finales de los años 90, es una modalidad educativa donde el estudiante tiene un papel activo y el docente desempeña el rol de tutor concentrado en el objetivo del aprendizaje.
Esa instrucción en línea se refiere a las estrategias virtuales como las que brindan las escenas interactivas creadas con DescartesJS que permiten a los docentes adaptarse a variadas situaciones de enseñanza y aprendizaje. A ese conjunto de herramientas, técnicas y metodologías, R. González (2015) lo denomina “mestizaje metodológico”, puesto que se tiene la posibilidad de controlar algunos aspectos del proceso, tales como el tiempo, lugar, ruta y ritmo. Combinar las Tecnologías de la Información y Comunicación -TIC- con aprendizaje presencial requiere de un modelo de inserción.
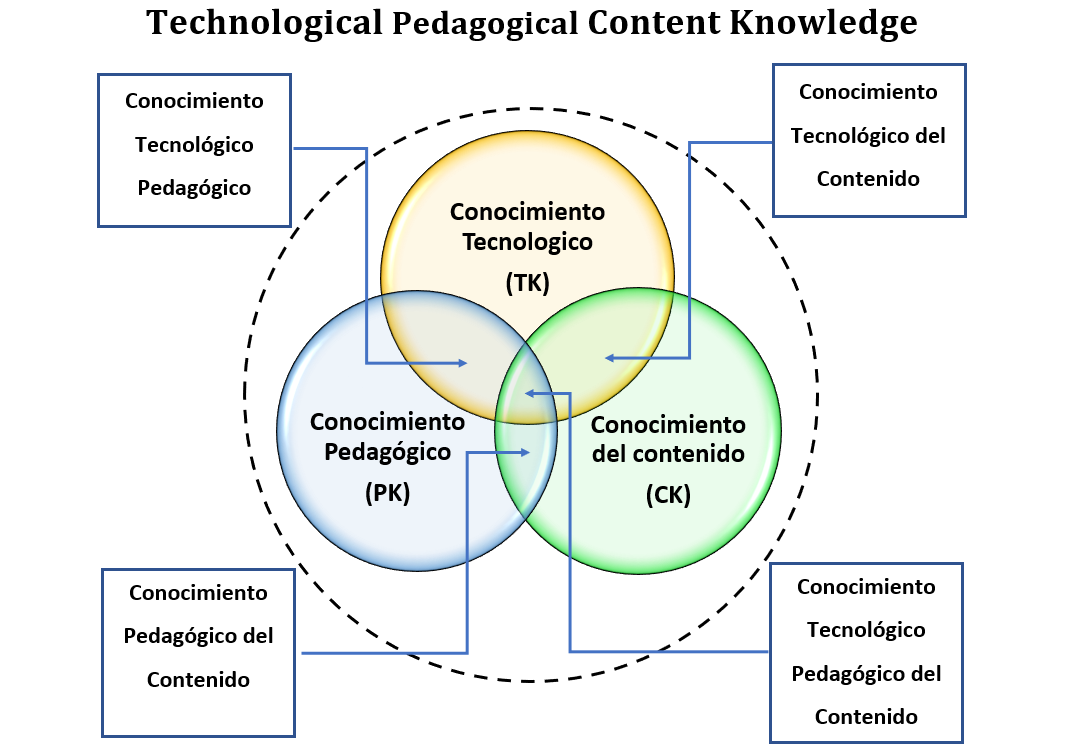
El modelo TPACK, acrónimo de “Technological Pedagogical Content Knowledge”, en español Conocimiento Técnico Peda- gógico del Contenido fue
Red Descartes 2021/Año 1, núm. 1
Red Descartes 2021/Año 1, núm. 1
Red Descartes 2021/Año 1, núm. 1
Escenas interactivas de DescartesJS en el aula híbrida
Con la siguiente escena motivadora creada para una clase híbrida de trigonometría detallaremos algunas estrategias para conseguir los siete conocimientos específicos que se obtienen de los tres conjuntos del modelo TPACK y sus intersecciones, tal como aparece en la ecuación 1:Red Descartes 2021/Año 1, núm. 1
- Conocimiento del contenido (el saber)
- Conocimiento pedagógico (cómo enseñar)
- Conocimiento tecnológico (cómo crear lo digital)
Lo anterior es el TPACK (Conocimiento Tecnológico Pedagógico del Contenido) que permite llevar el conocimiento a un aula híbrida en el área de trigonometría.
Antes de presionar los botones "Pista 1" o "Pista 2" se analizan las conjeturas presentadas por los estudiantes, que pueden llevar a establecer relaciones que satisfacen la pregunta motivadora.
En el marco de los géneros propuestos por los autores cita- dos encontramos: a) Considerar, b) Practicar, c) Interpretar, d) Pro- ducir, e) Evaluar y f) Crear. Una escena de DescartesJS se convierte en Objeto Interactivo de Aprendizaje -OIA- al incluir actividades en todos los géneros citados.
Una de esas actividades consiste en incluir en las escenas a crear, los textos necesarios donde el usuario pueda extraer información acerca de los conocimientos previos del saber teórico o conocimientos nuevos.
DescartesJS permite incluir enlaces para explorar o investigar un concepto usando Internet u otras fuentes de investigación externas o diseñar actividades dentro de la escena para incursionar en los géneros descritos.
Red Descartes 2021/Año 1, núm. 1
Continuando con las bondades de las escenas creadas con Descartes para facilitar el aprendizaje híbrido en el marco del modelo TPACK dentro del aula podemos afirmar que el usuario, asistido por la tecnología en el proceso de descripción o documentación, adquiere la capacidad de producir una explicación matemática de un objeto o concepto y de las posibilidades de la animación o simulación del movimiento inmerso en el OIA.
Una simulación es la explicación que le brinda al estudiante las herramientas para comprobar las conjeturas que se obtienen de una buena escena motivadora. De la comprobación de una conjetura específica planteada y de examinar la retroalimentación de resultados interactivos se derivan conocimientos al establecer las relaciones de los conceptos u objetos presentados en el OIA.
Lo descrito hasta el momento nos permite suponer que el denominado docente siglo XXI
- El pedagógico Hace referencia al diseño instruccional como Tecno- logía Educativa, al respecto Santos (2000) expresa que es el puente que conecta el conocimiento generado por las ciencias de la educación con las aplicaciones para resolver problemas del aprendizaje o también como la disciplina de las ciencias de la educación, vinculada a los medios tecnológicos, la psicología educativa y la didáctica.
- El tecnológico Aquí se referencian las Tecnologías de la Informa- ción y la Comunicación (TIC), mediante la selección, personalización, diseño, im- plementación, alojamiento y mantenimiento de solu- ciones donde se integran tecnologías propietarias y de código abierto (Open Source).
Red Descartes 2021/Año 1, núm. 1
Aunque existen otros modelos tecnopedagógicos, el TPACK y DescartesJS son un complemento ideal para la enseñanza hibrida ya que esta herramienta de autor permite la incorporación eficiente de las herramientas digitales en el campo educativo por medio de los conocimientos tecnológico, pedagógico y disciplinar.
El conocimiento tecnológico reflejado en lenguajes de programación como lo es JavaScript y el lenguaje Html5, permite construcciones de interfaz web intuitiva y eficaz capaz de facilitar el proceso educativo en cualquier tema del conocimiento.
De igual manera podemos llevar la estrategia de la simulación asistida por lenguaje de com- putadora (Conocimiento Peda- gógico) orientada con el modelo
Referencias
Colvin, Ruth (2008). Building Expertise. John Wiley y Sons.González, R. (2015). Manual de emergencia para agentes de cambio educativo. México: Ediciones Granica.
Koheler, M. (2012). What is TPACK? Disponible en http://www.tpack.org.
Martínez, J. (2008). El arte de aprender… y enseñar. Manual para docentes. Santa Cruz de la Sierra: La Hoguera.
Grandgenett, N., Harris, J., y Hofer, M. (2011). Mathematics learning activity types.
Santos, A. (2000). La tecnología educativa ante el paradigma constructivista. Informática Educativa, 83-94.
Red Descartes 2021/Año 1, núm. 1
Química
ChemDoodle y DescartesJS
Juan Guillermo Rivera Berrío
Presentamos la biblioteca química de componentes web ChemDoodle, diseñada en Javascript y producida por iChemLabs. Estos componentes permiten al usuario presentar gráficos y animaciones 2D y 3D de calidad de publicación para estructuras químicas, reacciones y espectros. Más allá de los gráficos, esta herramienta proporciona un marco para la interacción del usuario para crear aplicaciones dinámicas a través de navegadores web, plataformas de escritorio y dispositivos móviles como iPhone, iPad y dispositivos Android. Esta biblioteca también tiene acceso completo a toda la API de escritorio ChemDoodle a través de AJAX, lo que permite un acceso rápido a uno de los paquetes de gráficos químicos más robustos que existen directamente a través de Javascript.
Un ejemplo se presenta en la siguiente página. Interactúa con la molécula, diseñada en ChemDoodle (debes ampliarla con la rueda del ratón, o hacer clic sostenido sobre la molecula para rotarla). Se trata de la molécula de la cafeína, $C_8H_{10}N_4O_2$, que es la suma de las masas atómicas de ocho átomos de carbono, diez átomos de hidrógeno, cuatro átomos de nitrógeno y dos átomos de oxígeno, lo que equivale a 194.19 uma.
En el libro interactivo "Química. Volumen I - Parte 1", publicado por nuestra Red, se hace uso de esta biblioteca. A lo largo del libro se incluyen objetos interactivos permitiendo que la química se vuelva más interesante y accesible para los estudiantes y manteniendo el rigor inherente a la materia.
Red Descartes 2021/Año 1, núm. 1
La biblioteca de componentes web de ChemDoodle tiene LICENCIA PÚBLICA GENERAL GNU. Si deseas incluir componentes web de ChemDoodle en un sitio web, debes cumplir con esta licencia. La versión 8.0, la puedes descargar desde aquí.
En el siguiente vídeo, te mostraremos cómo puedes diseñar otras moléculas para insertar en la web. Para ello, debes descargar el chemdoodle y el siguiente archivo html, que hemos llamado Transformer, el cual lo debes guardar en subcarpeta "samples" del chemdoodle que descargaste y descomprimiste.
Red Descartes 2021/Año 1, núm. 1
Vídeo
Como pudiste observar en el vídeo, el uso de DescartesJS se limitó a facilitar el copiado del archivo que define la molécula; sin embargo, hay otra utilidad del editor que permite convertir el archivo con un diseño "responsive", el cual se describe en otro apartado de esta revista.
A continuación, presentamos la molécula de la aspirina diseñada en el vídeo y, además, la molécula de la piedra alumbreLa piedra de alumbre es un mineral, sal a base de sulfato de potasio (alunitas), que se encuentra de forma natural en yacimientos de muchas regiones de todo el mundo, sobre todo en Siria y Oriente Medio. Se utiliza desde la antigüedad tanto en cosmética como para la limpieza de tejidos (https://www.enfemenino.com/)..
Red Descartes 2021/Año 1, núm. 1
Red Descartes 2021/Año 1, núm. 1
Ilusiones ópticas
The Flashed Face Distortion Effect
Juan Guillermo Rivera Berrío
En la siguiente escena interactiva se genera la ilusión de caras distorsionadas. El efecto, según sus autores, depende de las caras que se contraponen, por ello, en algunos casos, no se percibirá distorsión significativa (véase https://www.mbthompson.com/ o http://illusion- oftheyear.com/2012/, para más información).
Como muchos descubrimientos científicos interesantes, este fue un accidente. Sean Murphy, un estudiante universitario, estaba trabajando solo en el laboratorio en una serie de caras para uno de sus experimentos.
Red Descartes 2021/Año 1, núm. 1
Alineó un conjunto de caras a los ojos y comenzó a examinarlos. Después de unos segundos, notó que algunas de las caras comenzaron a aparecer muy deformadas y grotescas. Miró las caras especialmente feas de forma individual, pero cada una de ellas parecía normal o incluso atractiva. Lo llamamos el "efecto de distorsión de la cara parpadeante" y queríamos compartirlo con el mundo, así que lo pusimos en YouTube.
El efecto parece depender del procesamiento de cada cara a la luz de las otras. Al alinear las caras en los ojos y presentarlas rápidamente, resulta mucho más fácil compararlas, por lo que las diferencias entre las caras son más extremas. Si alguien tiene una mandíbula grande, se ve casi como un ogro. Si tienen una frente especialmente grande, entonces se ve particularmente bulbosa. Estamos realizando varios experimentos en este momento para descubrir exactamente qué está causando este efecto, ¡así que mira este espacio! (https://www.mbthompson.com/).
Los estudios de la percepción visual han demostrado que nuestro cerebro tiende a generar imágenes a través de procesos de menor esfuerzo que, en consecuencia, producen perceptos errados del fenómeno observado. Estos errores se hacen más notorios cuando existen elementos distorsionadores de la realidad.
En el libro interactivo Percepción Visual, presentamos esta ilusión visual y más de un centenar de ilusiones adicionales.
Red Descartes 2021/Año 1, núm. 1
Difusión
¿Por qué me gusta Descartes?
José Antonio Salgueiro González
Coincidiendo con el 8º aniversario de RED Descartes, y con el objetivo de actualizar algunas de nuestras producciones audiovisuales, hemos decidido editar y compartir con todos nuestros usuarios y seguidores el siguiente vídeo, que hemos denominado ¿Por qué me gusta Descartes?, donde socios y miembros de la RED Descartes de cinco países responden escuetamente a la pregunta formulada aportando su personal valoración, además de poner rostro y voz a nuestra red con una representación de la misma. Una red docente bien conectada que, con sólidos pilares asentados entre Colombia, España y México, se va extendiendo a otros países de lenguas hispana y portuguesa.
Red Descartes 2021/Año 1, núm. 1
Desde Brasil, Colombia, Costa Rica, España y México, podemos conocer las valoraciones de diferentes perfiles o roles en RED Descartes, como desarrollador y documentalista de la herramienta de autor Descartes JS y del código para la edición y diseño de libros interactivos, autores y creadores de recursos educativos abiertos con Descartes JS y sus libros interactivos, coordinadores y formadores del programa de Educación Abierta, traductor de los recursos a portugués de Brasil y docentes de primaria, secundaria obligatoria, bachillerato y universidad de distintas especialidades.
Trabajar de forma altruista para y por la comunidad educativa de la aldea global
Además, han desempeñado funcio- nes de tutorización o coordinación de cursos de formación en línea de INTEF y de sus administraciones autonómicas respectivas y, hoy en día, constituidos como organización no gubernamental, ponen todos sus conocimientos y empeño en trabajar de forma altruista para y por la comunidad educativa de la aldea global, lema de RED Descartes.
Red Descartes 2021/Año 1, núm. 1
DescartesJS
DescartesJS con diseño adaptable
Juan Guillermo Rivera Berrío y Edison Arbey Escobar Acevedo
El diseño web adaptable, también conocido como diseño web adaptativo o responsivo (del inglés responsive web design) es, según Martínez (2013)Martínez, E. L., & Ceballos, C. S. (2013). Diseño web adaptativo o responsivo., una técnica de diseño y desarrollo web que, mediante el uso de estructuras e imágenes fluidas, así como de media-queries en la hoja de estilo CSS, consigue adaptar el sitio web al entorno del usuario.
Hoy los sitios web son vistos en dispositivos como tabletas, teléfonos inteligentes, libros electrónicos, portátiles, televisores, entre otros. Esto conlleva un problema en el diseño web, y en el diseño de escenas interactivas, ya que cada dispositivo tiene sus especificaciones técnicas particulares como son el tamaño de pantalla, su resolución en píxeles, la potencia de la CPU y la GPU, la memoria RAM, el sistema operativo, el software que soporta, entre otros elementos. Frente a estas diferencias, el diseño adaptativo es la mejor respuesta y/o solución ya que con un único diseño todo se ve y funciona correctamente independiente del dispositivo.
Según Wikipedia, fue el diseñador y autor norteamericano Ethan Marcotte quien creó y difundió esta técnica a partir de una serie de artículos en A List Apart. Una publicación en línea especializada en diseño y desarrollo web, idea que luego amplió en su libro Responsive Web Design publicado en el 2011. Hoy esta técnica es considerada un paradigma en el diseño web.
Red Descartes 2021/Año 1, núm. 1
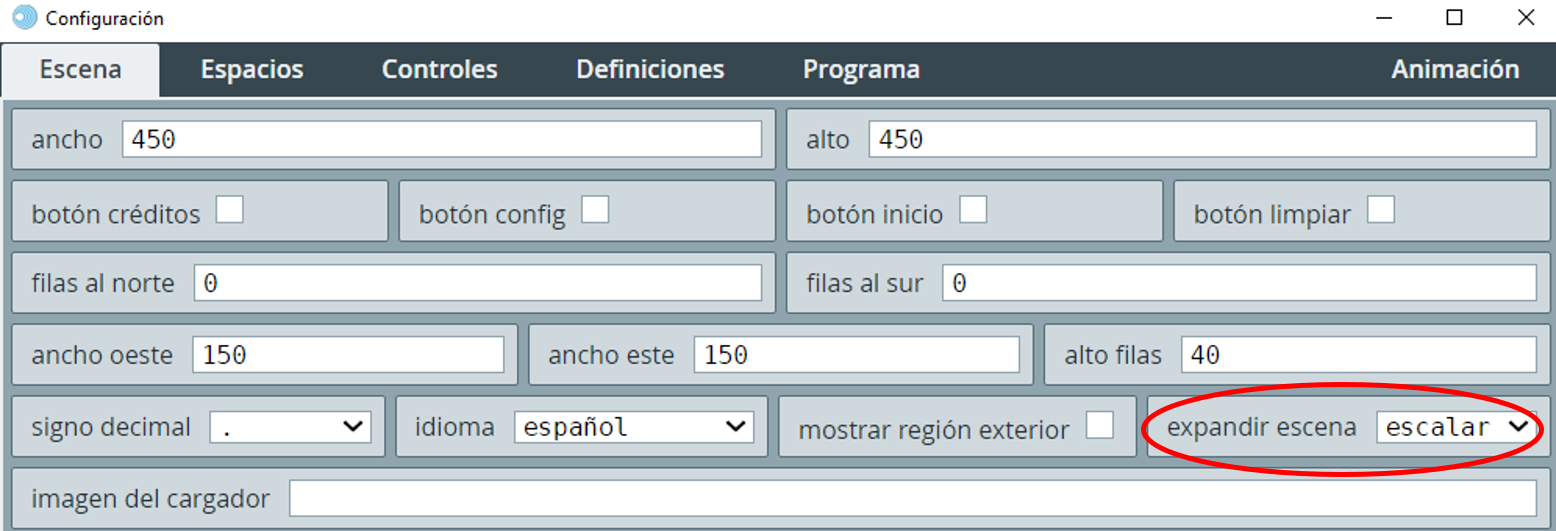En DescartesJS es posible escalar las escenas al tamaño del contenedor o, si se prefiere, adaptarlas al contenedor. Para ello, en el selector "Escena", en la opción expandir escena, se selecciona escalar.
Observa el vídeo, en el que insertamos una escena HTML correspon- diente a una molécula de química y, luego, le aplica- mos el diseño adaptable (Haz clic en el botón de pantalla completa).
He aquí el resultado (haz clic en la esquina superior derecha)
Red Descartes 2021/Año 1, núm. 1
Divulgación
Creación de un Aula de Futuro en Lebrija (España)
Manuel Muñoz Cañadas
El Aula del Futuro es un proyecto coordinado por el INTEF, en colaboración con las comunidades autónomas de España, que apuesta por potenciar el uso de las metodologías activas para el desarrollo competencial del alumnado. Para ello, se apuesta por explotar las posibilidades que nos ofrecen las tecnologías digitales y los espacios disponibles en los centros educativos (Véase https://intef.es/tecnologia-educativa/, para más información).
Vemos la entrevista realizada por Lebrija TV a la directora del CEP y colaboradores, para saber más sobre la instalación del aula.
Red Descartes 2021/Año 1, núm. 1
En el CEP de Lebrija se ha creado un Aula de Futuro que propone una metodología innovadora dentro de un espacio de aprendizaje tecnológico.
Red Descartes 2021/Año 1, núm. 1
El aula y sus orígenes
Presentación del aula
Observa el siguiente interactivo DescartesJS:
Dotación del aula
Orígenes del AdF
Los orígenes de este proyecto se remontan a 2012, con el inicio del proyecto Future Classroom Lab (FCL), de- sarrollado por el consorcio de Ministerios de Educación euro- peos, European Schoolnet (EUN), y que surge de los resultados obtenidos del pro- yecto de investigación y desa- rrollo iTEC. En 2015 se creó la red de embajadores del Aula del Futuro (AdF) en colaboración con las comunidades autóno- mas. En 2017, el entonces Mi- nisterio de Educación, Cultura y Deporte, inauguró el Aula del Futuro del INTEF, con vista a ofrecer oportunidades de for- mación y desarrollo profesional docente. Para ello y siguiendo el modelo europeo, se planteó una división, en seis zonas, muy similar a la del aula de Bruselas. Fuente de información.
Red Descartes 2021/Año 1, núm. 1
Puntos a resaltar
Red Descartes 2021/Año 1, núm. 1
Guía para los autores
Características de los artículos
- El autor puede presentar el artículo en un documento de texto con un máximo de ocho paginas en Arial tamaño 12.
- Si el autor tiene competencias en el diseño HTML y CSS, puede usar la plantilla de la revista, con un máximo de 10 páginas.
- El título será menor a 150 caracteres.
- Las imágenes, figuras, tablas, videos y objetos interactivos, se deben enviar en un archivo zip aparte.
- Idioma. La revista acepta artículos en español, inglés y portugués.
- Los artículos, preferiblemente, se relacionarán con aspectos educativos y el uso de las tecnologías en los procesos de enseñanza-aprendizaje. No obstante, se aceptan artículos de otras áreas del conocimiento, siempre que estos incorporen contenidos digitales diseñados con el editor DescartesJS.
- Presentar los permisos para el uso de contenido sujeto a derechos de autor, incluyendo los que provienen de Internet.
El artículo y los anexos deben enviarse en una archivo zip, a través de un enlace (vía hosting o Google Drive, por ejemplo).
Los artículos deben abordar temas como:
- Difusión relacionada con la Red Educativa Digital Descartes
Red Descartes 2021/Año 1, núm. 1
- Reseñas de libros interactivos
- Aplicaciones con DescartesJS
- Novedades DescartesJS
- Experiencias en el aula
- Investigaciones que incluyan el uso de contenidos digitales interactivos diseñados con DescartesJS
Evaluación de los artículos
El o los autores podrán sugerir revisores, indicando los datos de contacto (nombre y dirección de correo).
Los editores del Consejo Editorial, en primera instancia, valorarán los artículos para verificar que cumplen con los objetivos de publicación de la revista, si el concepto es positivo se asignarán mínimo dos revisores quienes evaluarán el artículo y harán las recomendaciones pertinentes, entre ellas la aceptación o no de su publicación.
